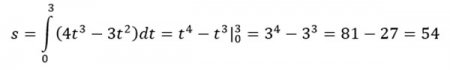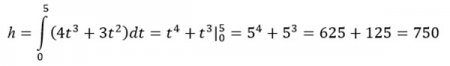Прикладные задачи для проведения самостоятельных и контрольных работ в классах естественнонаучного профиля

При организации контроля освоения учебного материала по теме "Определенный интеграл" учитель может предложить обучающимся задачи математического содержания т.к. на изучение данной темы отводится небольшое количество часов.

Но учитель может использовать и нетрадиционные формы контроля: участие в деловых играх и семинарах, самостоятельная разработка прикладных задач с последующим их анализом.

Все это способствует развитию у школьников навыка видеть проявление математических закономерностей в повседневной жизни, активно применять математические методы для решения задач в различных областях.

Рассмотрим задачи, которые учитель может предложить обучающимся для самостоятельного решения или включить их в контрольную работу.

Задача 1

Заяц пересекает открытое поле со скоростью v=v(t) (время измеряется в секундах, а скорость в метрах за секунду). Какова длина пройденного пути по полю, если заяц пересек его за 3 секунды со скоростью v(t)=4t³-3t², считая от начала движения t=0.

Решение:

Решение задачи 1

Необходимо определить путь, пройденный зайцем за промежуток времени [0;3].

Ответ: длина пройденного пути 54 метра. Средняя скорость зайца составляет 18 м/с.

Задача 2

Орел, высматривая свою добычу, парит высоко над землѐй. Определите, на какой высоте находится орел, если от земли он поднимается за 5 секунд со скоростью, определяемой по формуле v(t)=4t³+3t².

Высоту, можно рассматривать как путь, преодоленный орлом за 5 секунд.
Решение:

Решение задачи 2

Ответ: орел находится на высоте 750 метров.

Задача 3

Рассмотрим в атмосфере вертикальный столб воздуха с постоянным сечением S см². Плотность воздуха ρ г/см³ зависит от высоты h над поверхностью земли. Записать формулу, для вычисления массы воздуха в столбе от высоты h₁ до h₂.

Решение:
Атмосферное давление меняется с высотой, следовательно, плотность воздуха является функцией высоты – ρ(h). Для вычисления массы воздуха необходимо составить следующую формулу:

Формула вычисления массы воздуха

Задача 4

Из одного килограмма древесины выходим, примерно, 300 грамм бумаги. Сколько килограмм бумаги получится из бревна ели длиной 12 метров и неоднородной плотностью ρ=ρ(x),ρ(x)=x²-5x (плотность выражается в кг/м³).

Решение:
Для начала необходимо определить массу бревна, а затем рассчитать выход бумаги.

Решение задачи 4

Получаем, что масса бревна ели 216 кг. Теперь узнаем выход бумаги из этого бревна.
216 ∙ 300 = 64 800 гр = 64,8 кг.

Ответ: из бревна ели длиной 12 метров получится 64,8 кг бумаги.

Задача 5

Клен считается умеренно растущим деревом. За год прирост дерева составляет 0,4 – 0,5 метров. Скорость роста зависит от природных условий и погодных факторов и определяется формулой v(t)=1/√t (скорость роста выражается в м/год). Какой высоты достигнуты саженцы клена, длиной 0,5 метра, через 8 лет?

Решение:

Решение задачи 5

Итак, за 8 лет клен вырос на 4 метра. Первоначальная длина составляла 0,5 метра. Следовательно, длина деревьев составляет 4,5 метров.
Ответ: высота деревьев равна 4,5 метров.

В современном мире нужны активные формы и методы обучения, при которых перед обучающимися ставятся жизненные задачи, требующие одновременного применения теоретических знаний и быстрого выполнения практических действий.

Такой подход ведет к формированию неподдельного интереса к математике и является залогом ее успешного изучения, также способствует формированию общих и профессиональных компетенций будущих специалистов.