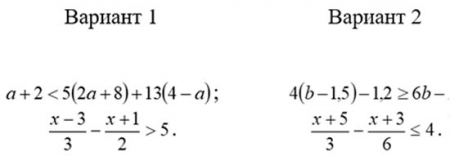Конспект урока математики в 8 классе "Решение линейных неравенств"

Главная » Средние классы » Конспекты уроков » Математика 8 класс

Цель урока: формирование и контроль уровня усвоения знаний, умений и навыков решения линейных неравенств.

Планируемые результаты:

умение точно и грамотно выражать свои мысли в устной и письменной речи, применяя математическую терминологию и символику, использовать различные языки математики (словесный, символический, графический);
выполнять арифметические преобразования, применять их для решения учебных математических задач;
пользоваться изученными математическими формулами;
применять свойства числовых неравенств для решения линейных неравенств.

Оборудование: меловая и интерактивная доски, компьютер, проектор, набор дидактических материалов для урока.

Ход урока

Организационный момент

- Ребята, сегодня мы, используя свойства числовых неравенств, получим алгоритм решения неравенства с одной переменной.

Проверка домашнего задания

Разбор заданий, с которыми не справилось большинство учащихся.

Актуализация знаний

- Освежим в памяти материал предыдущего урока. Вспомним понятия числового промежутка и свойств числовых неравенств.
- Для этого вам предлагается устно выполнить следующие задания. Читаю каждое задание и спрашиваю учащихся.
- В процессе выполнения, если это необходимо, обращаюсь к классу с вопросом: какие затруднения вызывают задания? И быстро объясняю решения.

1. Принадлежит ли промежутку [-3,6; 3,5] число:
а) -3,6 (да)
б) -3.5 (да)
в) -1 (да)
г) 0 (да)
д) 2,4 (да)
е) 3 (да)

2. Какие из целых чисел принадлежат промежутку?
а) (-2,5;3,4) ответ: -2,-1,0,1,2,3
б) (-0,2;0,7) ответ: 0
в) [-4;2,5] ответ: -4,-3,-2,-1,0,1,2
г) [-4,4;0] ответ: -4,-3,-2,-1,0
д) (-5;1) ответ: -4,-3,-2,-1,0,1
е) (-4;3) ответ: -4,-3,-2,-1,0,1,2

3. Указать наибольшее и наименьшее целое число, принадлежащее промежутку:
а) (-5;13) ответ: 12,-4
б) (-7;-1) ответ: 0,-6
в) [-3;0,7] ответ: 0,-3
г) [-18;1,8] ответ: 1,-18

4. Принадлежит ли промежутку [2,7;7] число:
а) 3 (нет)
б) 5 (да)
в) 12 (да)
г) 15 (да)
д) 36 (да)
е) 49 (да)

- Как применять свойства числовых неравенств при решении неравенств с одним неизвестным? (учащиеся встречаются с затруднением, составляют план по разрешению создавшегося затруднения)

Изучение нового материала

- Какие свойства неравенств вы знаете? (учащиеся перечисляют)

Если из одной части неравенства перенести в другую слагаемое с противоположным знаком, то получится равносильное ему неравенство;
Если обе части неравенства умножить или разделить на одно и то же положительное число, то получится равносильное ему неравенство;
Если обе части неравенства умножить или разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный, то получится равносильное ему неравенство.

- Вспомним, как решали линейные уравнения. Решим уравнение:
2x + 4 = 8
2x = 8 - 4

- Какое свойство вы использовали?
2x = 4
x = 2

- Каким свойством пользовались здесь?
- А теперь решим неравенство: 18 + 6x > 0
- Каким свойством необходимо воспользоваться, чтобы выразить слагаемое, содержащее x?
6x > -18
- Воспользуемся еще одним известным вам свойством, чтобы выразить x
x > -3
Множество решений неравенства представляет собой открытый числовой луч (-3; +∞), который изображаем следующим образом:

Открытый числовой луч

Ответ: (-3; +∞)

- Неравенство 5x − 11 > 3 при одних значениях переменной x обращается в верное числовое неравенство, а при других нет. Например, если вместо x подставить число 4, то получится верное неравенство 5 x 4 − 11 > 3 , а если подставить число 2 , то получится неравенство 5 x 2 − 11 > 3 , которое не является верным.

- Говорят, что число 4 является решением неравенства 5x − 11 > 3 или удовлетворяет этому неравенству. Нетрудно проверить, что решениями неравенства являются, например, числа 100, 180, 1000. Числа 2;0,5;−5 не являются решениями этого неравенства.

- Запишем определения.

Линейным неравенством с одной переменной x называют неравенство вида a · x + b > 0, где вместо знака > может быть любой другой знак неравенства (<, ≤, ≥), а a и b – действительные числа, причем a ≠ 0

Решением неравенства с одной переменной называется значение переменной, которое обращает его в верное числовое неравенство.

Решить неравенство – значит найти все его решения или доказать, что решений нет.

Неравенства, имеющие одни и те же решения или не имеющие решений, называются равносильными.

- А теперь выделим алгоритм решения линейного неравенства с одним неизвестным:

Раскрыть скобки, имеющиеся с обеих частях уравнения.
Перенести члены, содержащие неизвестную величину, в левую часть, а члены, не содержащие неизвестную величину, - в правую (свойство 1).
Разделить обе части неравенства на коэффициент при неизвестном, если он не равен нулю (свойство 2).

Закрепление и систематизация знаний

Привожу примеры решения неравенств по алгоритму с подробным объяснением.

Пример 1. Решим неравенство 16x > 13x + 45.

Перенесем слагаемое 13x с противоположным знаком в левую часть неравенства: 16x − 13x > 45
Приведем подобные члены: 3x > 45
Разделим обе части неравенства на 3: x > 15

Множество решений неравенства состоим из всех чисел, больших 15. Это множество представляет собой открытый числовой луч (15;+∞), который можно изобразить:

Числовой луч

Ответ можно записать в виде числового промежутка (15;+∞).

Следующие два примера решают у доски учащиеся, комментируя.

Пример 2. Решим неравенство 15x - 23(x +1) > 2x + 11

Раскроем скобки в левой части неравенства: 15x − 23x - 23 > 2x + 11
Перенесем с противоположными знаками слагаемое 2x из правой части неравенства в левую, а слагаемое − 23 из левой части в правую и приведем подобные члены:
15x - 23x - 2x > 11 + 23
-10x > 34

Разделим обе части на −10 , при этом изменим знак неравенства на противоположный: x < -3,4.
Множество решений данного неравенства представляет собой открытый числовой луч (-∞; -3,4), который можно изобразить следующим образом:

Графическое решение примера 2

Ответ: (-∞; -3,4).

В приведенных примерах мы получали линейные неравенства, в которых коэффициент при переменной не равен нулю. Может случиться, что при решении неравенств мы придем к линейному неравенству вида 0 · x > b или 0 · x < b.

Неравенство такого вида, а значит и соответствующее исходное неравенство либо не имеют решений, либо их решением является любое число.

Привожу пример неравенства такого вида, объясняя его решение.

Пример 3. Решим неравенство 2(x + 8) − 5x < 4 − 3x.

Имеем:
2x +16 − 5x < 4 − 3x
2x − 5x + 3x < 4 − 16

Приведем подобные члены в левой части неравенства и запишем результат в виде 0 · x: 0 · x < -12.
Полученное неравенство не имеет решений, так как при любом значении x оно обращается в числовое неравенство 0 < -12, не являющееся верным. Значит, не имеет решений и равносильное ему заданное неравенство.

Ответ: решений нет.

Контроль усвоения нового материала

- А теперь с учетом ранее допущенных ошибок, выяснения всех особенностей решений линейных неравенств, вам предлагается выполнить самостоятельную работу по вариантам. На доске написаны задания для двух.

Решить неравенства и изобразить множества их решений на координатной прямой.

Решите неравенства

На работу учащимся дается 15 минут. После сбора работ открываю на переносных досках решение самостоятельной работы. Ребята проверяют, где они допустили ошибки; отвечаю на вопросы учащихся.

Итоги урока. Рефлексия

- Что называется решением неравенства?
- Что значит решить неравенство?
- Каков алгоритм решения линейных неравенств?

- При выполнении каких заданий вы ошиблись? Почему?
- Укажите причины успехов и неудач своей деятельности на уроке.
- Продолжите высказывания об уроке: