Конспект урока геометрии 9 класс "От свойства к признаку. Исследование обратной теоремы для замечательных точек треугольника"

Методическая разработка урока построена в формате проблемного диалога и исследовательской деятельности.

Материал направлен на формирование понимания обратимости геометрических утверждений и логической строгости доказательств.

Урок геометрии с интерактивной доской

Цель:

• организовать деятельность учащихся по исследованию обратимости геометрических утверждений на примере теоремы о точке пересечения биссектрис треугольника;
• сформировать умение различать свойство и признак.

Задачи:

• сформировать понимание различий между свойством и признаком;
• научить формулировать обратную теорему;
• развить навыки проверки истинности утверждений;
• формировать логическое и критическое мышление.

Базовый учебник: Геометрия, 7–9 класс (Л.С. Атанасян и др.)

Оборудование: ПК, проектор, интерактивная доска, программа GeoGebra, раздаточный материал, чертежные инструменты.

Ход урока

Организационный момент. Создание мотивации

Учитель: Ребята, мы часто в геометрии доказываем теоремы вида: Если фигура обладает свойством А, то для нее верно следствие В.
- Например: Если треугольник равнобедренный, то углы при основании равны.

- Сегодня мы совершим поворот на 180 градусов. Мы будем не применять теоремы, а исследовать их логическую "прочность".
- Наша цель - понять, можно ли по следствию восстановить свойство, и что для этого нужно. Это урок для настоящих математических детективов".

Актуализация опорных знаний

Фронтальная беседа у доски:

1. Сформулируйте теорему о свойстве биссектрисы угла. (Точка, лежащая на биссектрисе, равноудалена от сторон угла)
2. Сформулируйте теорему о точке пересечения биссектрис треугольника. (Биссектрисы треугольника пересекаются в одной точке, которая является центром вписанной окружности)
3. Что такое вписанная окружность в треугольник? (Окружность, касающаяся всех трех его сторон)

Вывод

Прямая теорема: Если в треугольнике провести три биссектрисы, то они пересекутся в одной точке, равноудаленной от всех сторон, то есть в центре вписанной окружности. (Свойство → Центр вписанной окружности)

Постановка учебной проблемы

Учитель записывает на доске "Прямая теорема" и ее краткую схему.
- Теперь давайте "перевернем" эту мысль. Попробуем сформулировать обратное утверждение. Если в треугольнике существует точка, равноудаленная от всех сторон (т.е. являющаяся центром вписанной окружности), обязательно ли она является точкой пересечения его биссектрис?

- Иными словами, верна ли обратная теорема... (Центр вписанной окружности → Свойство биссектрис)
Ученики высказывают первые интуитивные предположения, чаще всего "да".

Учитель: Интуиция в геометрии - хороший помощник, но не судья. Давайте проверим ее методами строгой науки.
- Ваша исследовательская задача на сегодня: выяснить, является ли равенство расстояний от точки до сторон треугольника признаком того, что эта точка лежит на биссектрисах. И если является, то всегда ли?

Первичное исследование. Поиск контрпримера

Групповая работа

Класс делится на группы по 3-4 человека.

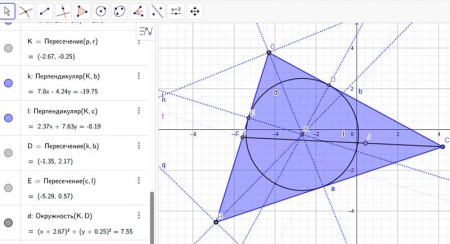
- Воспользуйтесь динамической геометрической средой GeoGebra (или постройте чертеж на бумаге). Постройте произвольный треугольник ABC.

- Постройте точку O внутри него. Опустите из точки O перпендикуляры на стороны треугольника. Измерьте их длины.
- Попробуйте перемещать точку O так, чтобы все три расстояния стали равны. Удалось ли вам? Где находится эта точка?

Ожидаемый результат: учащиеся экспериментально подтверждают, что внутри треугольника существует единственная точка, равноудаленная от сторон (центр вписанной окружности).

Учитель: Отлично! Значит, обратное утверждение кажется верным. Но математик должен быть дотошным.
- Вопрос на углубление: А если точка, равноудаленная от сторон, лежит вне треугольника?
- Или если расстояния равны, но точка лежит не внутри, а, например, напротив тупого угла?

Этап моделирования "особого случая"

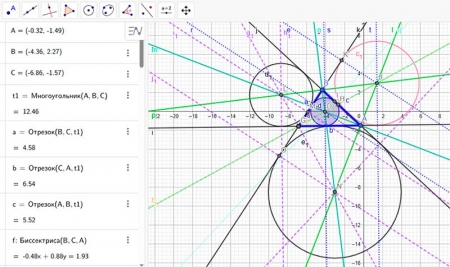
Учитель на интерактивной доске в GeoGebra показывает построение:

1. Строит остроугольный треугольник.
2. Строит точку O₁ - пересечение биссектрис (центр вписанной окружности). Все расстояния равны.
3. Строит точку O₂ - пересечение биссектрис внешних углов B и C. Эта точка также будет равноудалена от прямых AB, BC и CA, но окажется вне треугольника. Это - центр одной из вневписанных окружностей.

Наглядный вывод: оказывается, точек, равноудаленных от трех прямых (сторон треугольника), может быть четыре: одна внутри и три вне. Это контрпример к грубой формулировке "равноудаленная точка → центр вписанной окружности".

Построение графика в программе GeoGebra

Формулировка гипотезы и признака

Учитель: Итак, наше первоначальное обратное утверждение оказалось неполным. Мы нашли дополнительное условие, которое отделяет нужную нам точку от других.
- Какое это условие? (Точка должна находиться внутри треугольника)

- Верно! Но достаточно ли этого? (Ответы учащихся)
- Рассмотрим точку, лежащую, например, на медиане. Можно ли ее "подвигать" так, чтобы расстояния до сторон стали равны, но она не попала на биссектрису?

Круг вписанный в треугольник

Обсуждение приводит к выводу: равенство расстояний (перпендикуляров) от внутренней точки до сторон однозначно означает, что эта точка лежит на всех трех биссектрисах углов треугольника. Это и есть признак точки пересечения биссектрис (центра вписанной окружности).

Совместное формулирование итога

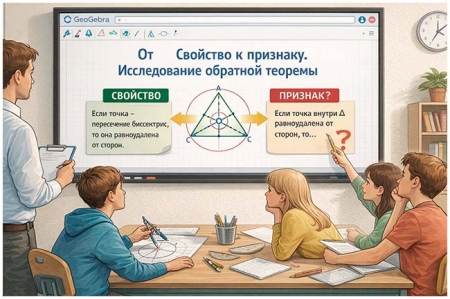
Ученики под руководством учителя сравнивают две формулировки:

1. Свойство (прямая теорема): Если точка - точка пересечения биссектрис треугольника, то она равноудалена от его сторон.
2. Признак (обратная теорема с условием): Если точка внутри треугольника равноудалена от его сторон, то она является точкой пересечения его биссектрис (центром вписанной окружности).

Первичное закрепление и рефлексия

Практическое задание (устно или письменно)

Даны два утверждения. Определите, какое из них - свойство, а какое - признак. Объясните, почему второе утверждение нуждается в уточнении.

а) Если четырехугольник - квадрат, то его диагонали равны.
б) Если в четырехугольнике диагонали равны, то это квадрат.

Обсуждение
Утверждение А - свойство квадрата. Утверждение Б - ложно как признак (есть контрпример: равнобедренная трапеция, прямоугольник). Нужны дополнительные условия (перпендикулярность, точка пересечения делится пополам и т.д.)

Итоговая рефлексия

- Какую главную логическую ошибку мы сегодня учились избегать? (Смешение свойства и признака)
- Почему в геометрии так важна точность формулировок? (Каждое слово ограничивает условия и отсекает контрпримеры)
- Где еще в математике можно применить сегодняшний исследовательский прием? (Исследование обратимости теорем о параллельных прямых, свойствах параллелограмма и т.д.)

Домашнее задание (дифференцированное)

Базовый уровень
Привести собственный пример геометрического свойства и попытаться сформулировать для него обратное утверждение. Проверить, верно ли оно.

Продвинутый уровень
Провести аналогичное исследование для теоремы о серединном перпендикуляре: Если точка лежит на серединном перпендикуляре к отрезку, то она равноудалена от концов отрезка.

- Всегда ли верно обратное?
- В каком случае верно?
- Сформулируйте признак точки, лежащей на серединном перпендикуляре