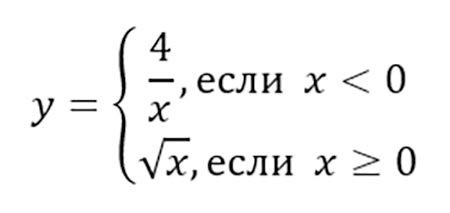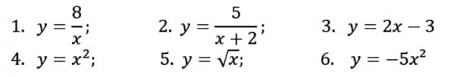Конспект урока алгебры 9 класс "Графики функций. Использование табличного процессора Exсel для построения графиков функций"

Главная » Старшие классы » Конспекты уроков » Математика 9 класс

Формируемые результаты:

формировать умение строить графики функций; функций, заданных кусочно;
развивать готовность к самообразованию и решению творческих задач;
строить графики функций с использованием табличного процессора Exсel.

Основные понятия: функция, прямая и обратная пропорциональности, парабола, гипербола, ветви гиперболы, ветви параболы, область определения, множество значений, графический редактор.

Ход урока

Организационный момент

Тема, цель урока (учащиеся знакомы с понятием "синквейн"). По предложенным фразам определить тему урока, затем обозначить цель урока.

Синквейн:

Линия.
Плавная, бесконечная.
Построить, определить, начертить.
Расположение зависит от коэффициента.
Зависимость.

Тема урока: "Графики функций. Использование табличного процессора Exсel для построения графиков функций".

В век цифровых технологий сидим, вычерчиваем линии, вычисляем координаты точек …
Как вы думаете, можно ли ускорить процесс построения графиков функций?
Мы попробуем сегодня с вами ответить на этот вопрос. А для начала вспомним все, что мы знаем о функциях.

Систематизация и обобщение материала

Устно:

Что называется функцией? (соответствие между двумя переменными, при котором каждому значению одной переменной соответствует единственное значение другой переменной)
Как другими словами называют независимую переменную? (аргумент)
Что называется областью определения? (значение, которое может принимать аргумент)
Что называется множеством значений? (соответствующие значения функции)
Что называется графиком функции? (множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, ординаты – соответствующим значениям функции)
С построением графиков каких функций мы уже знакомы?

y=kx+b – линейная функция (частный случай, когда k = 0 - прямая пропорциональность, или b = 0, прямая параллельна оси абсцисс), график – прямая;

y=k/x – обратная пропорциональность, график – гипербола;

y=x² – квадратичная функция, график – парабола;

у= √х – график – ветвь параболы (y = √x - один из частных случаев степенной функции. Эта функция не имеет своего собственного имени (в отличие от квадратичной функции или кубической функции) и называется просто формулой. График функции - ветвь параболы.

На слайде представлены графики перечисленных функций. Назовите основные свойства функций:

	у = кх+b	y = k/x	y = x²	y = √x
D(f)	R	Все числа, кроме х = 0	R	x ≥ 0
Е(f)	R	Все числа, кроме y = 0	y ≥ 0	y ≥ 0

Работа в тетрадях

(с последующей самопроверкой. Ответы представлены на слайде)

1. Найти область определения функций:

Найдите область определения функций

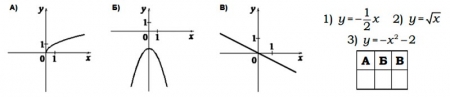
2. Установите соответствие между графиками функций и формулами, которые их задают.

Установите соответствие между графиками функций и формулами

3. Построить график одной из функций (можно на миллиметровой бумаге): 1) y =2 x; 2) y = 1/x; 3) y = x²

Для того, чтобы построить график любой функции, что необходимо сделать? (построить координатную плоскость, составить таблицу, отметить полученные точки на координатной плоскости и затем соединить точки линией)

Но, оказывается, что все это может за нас сделать компьютер.