Урок математики в 11 классе "Решение задач по теме "Объемы тел"

Цели урока: обобщить и систематизировать знания по теме "Объемы тел".

Задачи:

• Повторить и систематизировать формулы для вычисления объемов многогранников и тел вращения.
• Продолжить формирование навыков решения задач по теме.
• Учить приемам мыслительной деятельности, развивать кругозор.

Оборудование: презентация, карточки с заданиями.

Ход урока

Организационный момент

- Здравствуйте, ребята! Садитесь. Ребята, у нас сегодня с вами необычный урок в том смысле, что на уроке присутствуют мои коллеги.
- Но, мы с вами, как и всегда, работаем в том же режиме и в том же темпе. И я хочу, чтобы сегодня на уроке пищу получил не только ваш ум, но и ваше сердце и душа.
- Прежде чем начать урок, давайте в начале пожелаем друг другу хорошее настроение и настроим себя на плодотворную работу.

Формулировка темы урока и целей урока

- Ребята, давайте вспомним, что мы проходили на прошлых уроках? (Объемы тел)
- Объемы каких тел мы с вами проходили? (прямоугольного параллелепипеда, куба, призмы, пирамиды, цилиндра, конуса, шара)

- Известный швейцарский математик Джордж Пойа сказал: "Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их".

- Исходя из этого высказывания, давайте сформулируем тему сегодняшнего урока, а также цели урока. (Вы сказали, что на прошлых уроках мы проходили объемы тел, и придерживаясь слов Джорджа Пойа, мы будем решать задачи)
- Тема нашего урока "Решение задач по теме "Объемы тел".

Актуализация опорных знаний

- Для того чтобы успешно решать задачи, необходимо повторить основной теоретический материал.
- Сегодня это формулы для вычисления объемов тел. Посмотрите на экран. Вы должны сейчас сопоставить геометрические тела с формулой нахождения их объема. (Ученики сопоставляют)
- Какой фигуры нет на этом слайде? (Призмы, усеченного конуса)

Вопросы практического тура

• Как найти объем призмы? (V=Sh)
• Как найти объем пирамиды? (V = 1/3 Sh)
• Как найти объем конуса? (V = 1/3 πr² h)
• Как найти объем прямоугольного параллелепипеда? (V = abc)
• Как найти объем куба? (V = a³)
• Как найти объем цилиндра? (V = πr² h)
• Как найти объем шара? (V = 4/3 πr³)
• Как найти объем усеченного конуса? (V = 1/3 πh (r²+r₁²+rr₁)

- Отлично, мы все формулы на нахождение объемов тел вспомнили!

Ответьте на следующие вопросы:

1. Во сколько раз увеличится объем цилиндра, если его высоту увеличить в 2 раза? (В 2 раза)
2. Во сколько раз увеличится объем конуса, если радиус его основания увеличить в 1,5 раза? (В 2,25 раза)
3. Во сколько раз уменьшится объем шара, если его радиус уменьшить в 3 раза? (в 27 раз)
4. Что произойдет с объемом цилиндра, если радиус цилиндра увеличить в 3 раза, а высоту уменьшить в 5 раз? (Увеличится в 1,8 раза)
5. Что произойдет с объемом конуса, если его высоту увеличить в 8 раз, а радиус основания уменьшить в 4 раза? (Уменьшится в 2 раза)
6. В каком случае объем чашки станет больше, если высоту увеличить в 2 раза или если радиус увеличить в 2 раза? Во сколько раз?

Практическое задание

- Ребята, а сейчас я вам раздам по одному из геометрических тел, и вы должны сказать, какое тело вы получили и должны будете рассчитать объем этого геометрического тела.
- Для этой маленькой практической работы вы должны пользоваться линейкой. Вы мне скажите, что для этого вы должны измерить.

Решение задач по теме "Объемы тел"

- Как говорится "Тяжело в учении, легко на ЕГЭ". Так как в этом году вам предстоит сдавать экзамен, то мы будем решать задачи из сборника для подготовки к ЕГЭ.
- Мы рассмотрим сегодня некоторые 8 задания по теме "Объемы тел" из профильного уровня и 13 задания из базового уровня.

Задача 1. Цилиндр и конус имеют общие основание и высоту. Объем конуса равен 28. Найдите объем цилиндра.

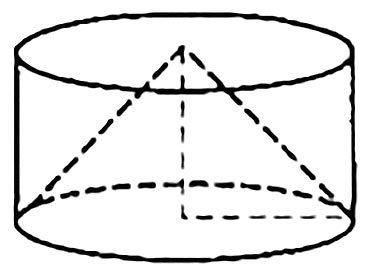
Алгоритм решения:

1. Записываем формулу объема конуса.
2. Записываем формулу объема цилиндра.
3. Сравниваем формулы, делаем вывод.
4. Вычисляем объем цилиндра.
5. Записываем ответ.

Решение:

1. Объем конуса определяем по формуле
V = 1/3 πr² h, где h – высота конуса; r – радиус основания конуса.

2. Объем цилиндра определяем по формуле
V_1 = πr² h = 3V

3. Сравниваем обе формулы. Легко видно, что объем цилиндра в 3 раза больше объема конуса.

4. Вычисляем объем цилиндра:
V_1 = 3 * 28 = 84

Ответ: 84.

Задача 2. Цилиндр описан около шара. Объем цилиндра равен 33. Найдите объем шара.

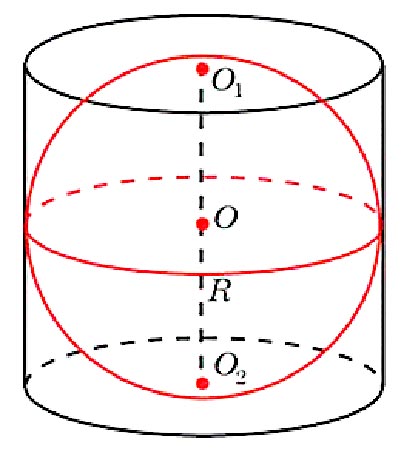
1. Запишем формулу объема цилиндра: V_ц=πr² h=33

2. Запишем формулу объема шара: V_ш=4/3 πr³

3. Мы видим, что радиус шара равен радиусу цилиндра, а высота цилиндра в 2 раза больше радиуса шара.

4. V_ц = πr² h = 2πr² r=2πr³ = 33 πr³ = 33/2
V_ш = 4/3 πr³ = (4∙33) / (3∙2) = 22

Ответ: 22.

- Можно заметить, что если цилиндр описан около шара или шар вписан в цилиндр, то V_ц = 3/2V_ш Или V_ш=2/3 V_ц

Задача 3. Задача, обратная данной. Шар объемом 28 вписан в цилиндр. Найти объем цилиндра.
Ответ: 42.

Задача 4. Объем конуса равен 12. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите объем отсеченного конуса.

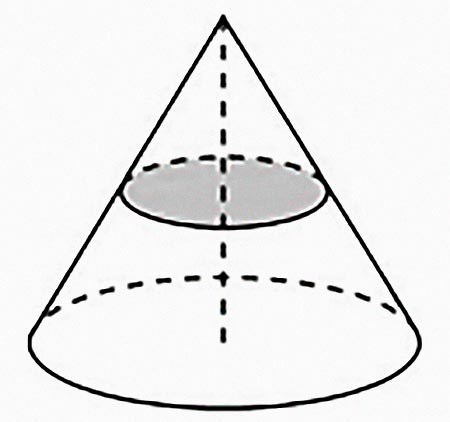
1. Запишем объем конуса: V = 1/3 πr² h = 12.

2. Запишем объем маленького конуса: V₁ = 1/3 πr₁² h₁

3. V = 1/3 πr² h = 1/3 π4r₁² 2h₁ = 8/3 πr₁²h  = 8∙1/3 πr₁²h₁ = 8∙V₁ = 12
Объем отсеченного конуса равен V₁ = 12/8 = 1,5
Ответ: 1,5.

- Можно заметить, что объем конуса равен 8-ми объемам конуса, отсеченного параллельно основанию и делящего высоту пополам.

Задача 5. В сосуде, имеющем форму конуса, уровень жидкости достигает 1/2 высоты. Объем жидкости равен 25 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?

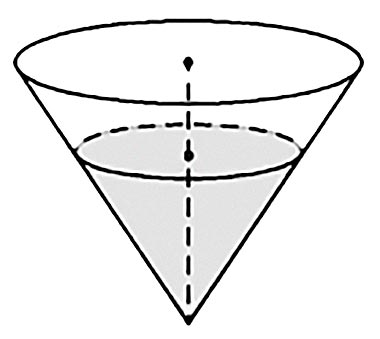
25*7 =175
Ответ: 175

Задача 6. Даны две кружки цилиндрической формы. Первая кружка в полтора раза ниже второй, а вторая вдвое шире первой. Во сколько раз объем второй кружки больше объема первой?

Две кружки цилиндрической формы

Решение.
Объем цилиндра вычисляется по формуле V=πr² h. Объем первой кружки равен V₁ = πr₁² h₁, объем второй кружки равен V₂=πr₂² h². Из условия задачи r₂=2r₁ и h₂=3/2 h₁ V₂/V₁ = (πr₂² h₂)/(πr₁² h₁ )= (4r₁² (3/2h)₁)/(r₁² h₁ ) = 6. Значит, объем второй кружки в шесть раз больше объема первой.
Ответ: 6.

Закрепление материала

- А теперь попробуйте решить следующие задачи по вариантам. Возьмите свои листы, которые я раздала перед началом урока, и решите их.

Задача 1. Цилиндр и конус имеют общие основание и высоту. Объем конуса равен 7. Найдите объем цилиндра. (21) (7*3=21)

Задача 2. Цилиндр и конус имеют общие основание и высоту. Объем цилиндра равен 18. Найдите объем конуса. (6) (18/3=6)

Задача 3. Шар, объем которого равен 72, вписан в цилиндр. Найдите объем цилиндра. (108) (72 * 3/2 =108)

Задача 4. Шар вписан в цилиндр. Объем цилиндра равен 21. Найдите объем шара. (14) (21*2/3=14)

Задача 5. В цилиндрический сосуд налили 500 см³ воды. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде увеличился в 1,2 раза. Чему равен объем детали? Ответ выразите в см³. (100) (500*0,2=100)

Задача 6. В сосуде, имеющем форму конуса, уровень жидкости достигает 0,5 высоты. Объем сосуда 1600 мл. Чему равен объем налитой жидкости? Ответ дайте в миллилитрах. (800) (1600:8=800)

- А теперь поменяемся тетрадями, и проверьте своих соседей по парте.
- Кто сделал всю работу без единой ошибки?
- Кто сделал одну (две) ошибку?

- Ребята, если вы допустили ошибки, значит вам надо работать еще над этими задачами.
- Составьте по одной любой задаче наподобие самостоятельной работы. Поменяемся тетрадями и решите задачу, которую составил сосед.

Рефлексия

Ребята по кругу высказываются одним предложением, выбирая начало фразы на рефлексивном экране на доске.

- Ребята, выберите начало любой фразы, и дополните ее, что вы узнали.

- Сегодня я узнал…

• Было интересно…
• Было трудно…
• Я выполнял задания…
• Я понял, что…

Домашнее задание

Подготовиться к контрольной работе. Решить 3 любых задач задания 8 из сборника егэ из профильного уровня или 3 задач задания 13 из базового уровня.

Египетские пирамиды – древнейшее и вместе с тем единственное сохранившееся до наших дней чудо света. Пирамида Хеопса – самая большая пирамида. Сейчас высота пирамиды составляет 137 м, основание 230 м * 230 м. Вычислите объем пирамиды. Округлите до десятых.

Выставление оценок

- Молодцы, все сегодня хорошо поработали. Спасибо всем за работу на уроке. Вам я желаю хорошо подготовиться и успешно сдать единый государственный экзамен.
- Урок окончен.

obemy-tel.rar

Размер:

73.82 Kb

Скачали:

176