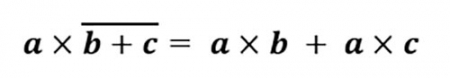Конспект урока математики 6 класс "Коэффициент. Распределительное свойство умножения"

Цели урока:

• формировать умения применять распределительное свойство умножения;
• развивать умение раскрывать скобки с помощью распределительного свойства умножения, используя правила раскрытия скобок;
• формировать первоначальные представления об идеях и о методах математики как об универсальном языке науки и техники.

Ход урока

Организационный момент

Учитель: Добрый день, сегодня мне бы хотелось начать со слов со слов нашего соотечественника Алексея Николаевича Крылова: "Рано или поздно всякая правильная математическая идея находит применение в том или ином деле".
- Вот и сегодня мы с вами убедимся в правильности данных слов.

- Прежде, чем перейти к теме нашего урока, давайте выполним следующие задания на повторение.

Устный счет

- Итак, вы справились с заданием. Посмотрите, какое слово у нас получилось? (отлично)
- Совершенно верно, именно так и не иначе вы сегодня справитесь со всеми заданиями.
- На прошлых уроках вы уже познакомились со свойствами действий с рациональными выражениями. Какое свойство вы изучили последним? (распределительное свойство умножения)

Учитель: Давайте вместе вспомним это свойство и запишем его на доске. (либо записываем, либо вешаем на доске напечатанный вариант)
- Как вы думаете, люди давно используют это свойство?

Историческая справка

Распределительное свойство умножения известно с глубокой древности, для его записи сначала использовали слова, затем, с введением букв, возникла потребность отделить каким-то образом выражение b + c, сегодня мы для этого используем круглые скобки.

Но круглые скобки появились впервые в XVI в. в трудах итальянского математика. (его имя мы узнаем в конце урока) Однако в течение почти всего XVII века употреблялись не скобки, а горизонтальная черта, проводимая над выражением, подлежащим включению в скобки.

Ученики того времени применяли такую запись распределительного свойства:

Формула распределительного свойства умножения

где "×" — знак умножения.

Работа по теме урока

Учитель: Сегодня мы с вами продолжим изучение темы "Распределительное свойство умножения".
- Откройте тетради, запишите сегодняшнее число и тему урока "Коэффициент. Распределительное свойство умножения". (Вешаем на доске название темы)
- Раз вы уже знакомы с данным свойством, то подумайте и скажите, какая цель нашего урока? (Научится применять данное свойство)

- Верно, цель нашего урока: научится применять распределительное свойство умножения рациональных чисел.
- А теперь, я вас попрошу достаточно быстро решить следующие примеры:

2 1/2∙2=?
9∙5 1/3=?

В чем возникло затруднение? Как вы пытались посчитать данный пример? (Ученики: переводили смешанное число в неправильную дробь и умножали)
- Может распределительное свойство нам поможет вычислить данный пример устно.
- Давайте представим смешанное число в виде суммы целого числа и дроби, а после применим распределительное свойство.

Ученики выполняют задания.
9∙(5+1/3) = 9∙5+9∙1/3=
45+9/3=45+3=48

- Т.е. мы сейчас с вами применяли распределительное свойство для раскрытия скобок. (вывешиваем на доске "Раскрытие скобок", "Умножение смешанного числа на целое число")
- Давайте закрепим это, и решим несколько заданий на раскрытие скобок, которые есть у вас на партах.

Раскройте скобки (решаем у доски)

• 2(a+3b)
• 3(a+2b-7c)
• m – (n + b)
• -0,4a(-4b + 3p – 1,1c)

Учитель: Замечательно, вы работаете, как я и предполагал, на отлично!

Физкультминутка

- А сейчас я предлагаю вам немножко отдохнуть и поиграть. Ваша задача – внимательно смотреть на числа, представленные на экране и выполнять следующие задания:

• Если число делится на 2 – руки вверх.
• Если число делится на 3 - руки вперед.
• Если число делится на 5 - хлопок в ладоши.

Числа: 46, 27, 35, 142, 234, 565, 813, 6660.
- Молодцы! Продолжим работу.

- Обратите внимание, что в теме нашего урока присутствует такое понятие, как коэффициент. Скажите, что это такое? (вешаю на доску слово коэффициент)

Коэффициентом называется числовой множитель при буквенном выражении

Учитель: Теперь давайте вспомним, как привести подобные слагаемые?
Ученики: Чтобы привести подобные слагаемые, нужно сложить коэффициенты и полученный результат умножить на общую буквенную часть.
Пример: 6x + 11x - 7x = 10x

Учитель: Давайте перейдем к практическому применению распределительного свойства.
- Сейчас я предлагаю вам решить старинную задачу XVIII века "Сколь он стар?".
Некто, будучи вопрошен, сколь он стар, ответствовал: "Когда я проживу еще половину, да треть, да четверть моих лет, тогда мне будет 100 лет". Сколь он стар?

- Решение автора данной задачи довольно замысловато и тяжело для восприятия. Я предлагаю решить ее с помощью уравнения. (у доски)
Решение:

- Составим уравнение: x + 1/2x + 1/3x + 1/4x = 100 и решим.
- На самом деле, приведение подобных членов – это применение распределительного свойства умножения.
- Ведь здесь мы выносим общий множитель x за скобки. (На доске вывешиваем "Вынесение общего множителя")

- Далее работаем в парах. На тех же листах с заданиями у вас есть подзаголовок "Работа в парах", где есть индивидуальное задание для каждого.
- Ваша задача выполнить свое задание в тетради, а полученный ответ сложить с ответом соседа по парте. Приступаем!

Раскройте скобки и упростите выражение (Учащиеся выполняют задание в течение 3-5 минут)
1 вариант: 2(3+11x)-(13x-8)
2 вариант: 2(8+3x)-(15x-12)
Учитель: Время вышло! Давайте проверим, какие ответы у вас получились! (42)
- Совершенно верно! - С данным числом связано достаточно много занимательных фактов, например, в культовом романе английского писателя Дугласа Адамса "Путеводитель для путешествующих автостопом по Галактике" дается ответ на "Главный вопрос жизни, Вселенной и всего такого".

- Этот ответ должен был решить все существующие в мире насущные проблемы. Специально созданный мощнейший во Вселенной суперкомпьютер искал его в процессе семи с половиной миллионов лет непрерывных вычислений, и его ждали все разумные расы.
- Когда этот ответ был, наконец получен, он гласил: "42". А, ведь еще это номер Вашей гостеприимной гимназии!

Учитель: Ребята, теперь давайте вспомним, что я рассказывал вам о том, когда и где впервые появились обозначения круглых скобок? (Ответы учащихся)
- А как звали того ученого-математика, который один из первых ввел данное обозначение? (Вы не говорили)
- Теперь, я считаю, пришло время выяснить это.

- У вас у каждого на столе лежит тест. Выберите правильный ответ и выпишите буквы выбранных ответов к каждому заданию на этом же листе.

Раскройте скобки

- Теперь давайте обменяемся своими тестами и проверим правильность ответов друг у друга.
- Если у вас в ответе получилась фамилия Тарталья, то вы все выполнили верно.
- Если есть, какие-то ошибки, то я вас попрошу в данном тесте зачеркнуть неверные ответы и поставить оценку по следующим критериям:

• От 1 до 3 правильных ответов – не получилось.
• От 4 до 5 правильных ответов – 3.
• От 6 до 7 правильных ответов – 4
• 8 правильных ответов – 5.

Никколо Тарталья - именно под такой фамилией нам известен итальянский математик-самоучка, который один из первых ввел обозначение круглой скоб.
Занимательно то, что настоящая его фамилия - Фонтана.

Домашнее задание
- И вот вам маленькое домашнее задание. Ответьте на вопрос "Что означает фамилия Тарталья, и почему ученого прозвали именно так?

Итог урока

Учитель: Что мы сегодня с вами закрепили?
Учащиеся: Понятие коэффициента, распределительное свойство, раскрытие скобок, вынос общего множителя.

Учитель: Вы хорошо работали, помогали друг другу и справились со всеми заданиями.
- Благодарю всех за активную работу и предлагаю оценить свою степень удовлетворенности работой на уроке.