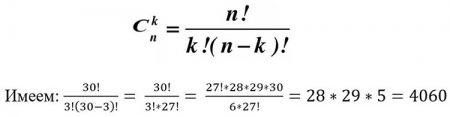Разбор заданий № 16 ЕГЭ по информатике повышенной сложности

Задание 1

Алгоритм вычисления значения функции F(n), где n — целое неотрицательное число, задан следующими соотношениями:

F(0) = 0;
F(n) = F(n − 1) + 1, если n нечетно;
F(n) = F(n / 2), если n > 0 и при этом n четно.

Укажите количество таких значений n < 1 000 000 000, для которых F(n)  =  3.

Решение

Если данную задачу решать "в лоб", то можно заметить, что перебираемое значение n слишком велико (109) и цикл "не пройдет" такое количество значений за короткое время. А значит, необходимо проанализировать саму функцию и разобраться, что она делает.

Не сложно понять, что данная рекурсивная функция подсчитывает число единиц в двоичной записи числа n. Для проверки запустим цикл n от 10 до 100 и для каждого такого n вызовем данную функцию:

def f(n):
   if n == 0:
     return 0
  elif n % 2 == 1:
    return f(n - 1) + 1
  elif n > 0 and n % 2 == 0:
    return f(n // 2)

  for i in range(10, 100):

    print(f'Десятичное число: {i}, Двоичное число: {bin(i)[2:]}, Число единиц: {f(i)}')

Получим:

Десятичное число: 10, двоичное число: 1010, число единиц: 2
Десятичное число: 11, двоичное число: 1011, число единиц: 3
Десятичное число: 12, двоичное число: 1100, число единиц: 2

Десятичное число: 13, двоичное число: 1101, число единиц: 3
Десятичное число: 14, двоичное число: 1110, число единиц: 3
Десятичное число: 15, двоичное число: 1111, число единиц: 4
…

Проверка показала, что наше утверждение верное.

Решить перебором данную задачу не получится из-за большого диапазона n. В задаче нам нужны все варианты чисел, которые в двоичном представлении имеют ровно 3 единицы, т.е. подойдут 111, 1011, 1101, 1110 и т.д.

Итак, нам нужно расставить 3 единицы всеми возможными способами на определенное число позиций. Чтобы понять, а на какое число позиций следует расставить 3 единицы, переведем максимально возможное число в заданном диапазоне в двоичную систему счисления и подсчитаем его длину:

print(len(bin(10**9 - 1)[2:]))

Получили число 30. Т.е. максимальное число в заданном диапазоне в двоичном представлении будем иметь 30 разрядов. Таким образом, нам следует разместить три единицы на 30 позициях всеми возможными способами. В этом нам поможет формула из комбинаторики подсчета числа сочетаний из n по k:

Формула подсчета числа сочетаний из n по k

Имеем: 30!/3!(30-3) != 30!/(3!*27!) = (27!*28*29*30)/(6*27!) = 28*29*5 = 4060

С помощью Python это сделать тоже не сложно:

import math
print(math.comb(30, 3))

Получим также ответ: 4060.

Однако, метод comb доступен для Python начиная с версии 3.8.

Задание 2

Алгоритм вычисления значения функции F(n), где n - целое неотрицательное число, задан следующими соотношениями:
Укажите количество таких чисел n из интервала 237 567 892 ⩽ n ⩽ 1 134 567 004, для которых F(n) не делится без остатка на 3.

Решение
Как и в предыдущей задаче, решение "в лоб" перебором будет невозможно. Запишем данную функцию и вызовем ее на промежутке от 1 до 100:
def f(n):
  if n == 0:
    return 0
  else:
    return f(n - 1) + n

  k = 0
  for i in range(1, 11):
    ans = f(i)
    print(f'Аргумент: {i}, Функция: {ans}, Остаток: {ans % 3}')
  if ans % 3 == 1:
    k += 1
  print(k)

Получим:
Аргумент: 1, функция: 1, остаток: 1
Аргумент: 2, функция: 3, остаток: 0

Аргумент: 3, функция: 6, остаток: 0
Аргумент: 4, функция: 10, остаток: 1
Аргумент: 5, функция: 15, остаток: 0

Аргумент: 6, функция: 21, остаток: 0
Аргумент: 7, функция: 28, остаток: 1
Аргумент: 8, функция: 36, остаток: 0
…

Мы видим, что функция возвращает сумму чисел от 1 до n. Причем, первое число (1) дает при делении на 3 остаток 1, а остатки для двух последующих чисел, возвращаемых функцией, равны нулю. Далее в остатках мы снова видим 1, 0, 0 и т.д. Докажем, что последующие выводы остатков будут аналогично повторяться.

Действительно, если рассмотреть последовательность: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, … можно заметить, что остаток от деления на 3 будет равен нулю каждое третье число. Запишем эти остатки: 1, 2, 0, 1, 2, 0, …

Но, т.к. мы последовательно складываем числа, то остаток суммы остатков равен остатку суммы исходных чисел. Поэтому, последовательность остатков сумм чисел при делении на 3 будет: 1, 0, 0, 1, 0, 0.

Это и подтвердилось выводом программы. А значит, f(n) в данной задаче не делится на 3, только тогда, когда остаток равен 1.
Нижняя граница (число 237 567 892) при делении на 3 дает остаток 1. А значит, можно применить формулу для вычисления всех таких чисел: (113 456 7004 - 237 567 892) // 3 + 1.

Реализуем решение на Python:

a = 237 567 892
b = 1134567004
print((b - a) // 3 + 1)

Ответ: 298999705.