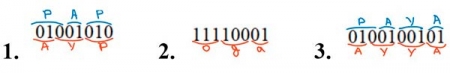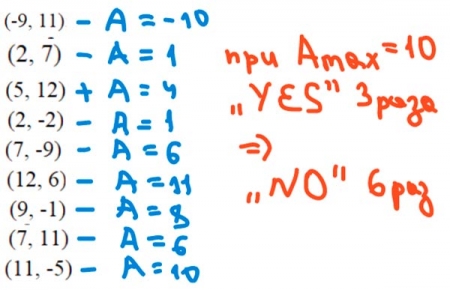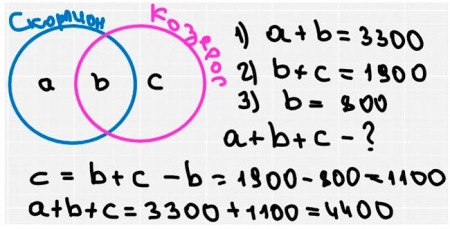Решение варианта диагностического тестирования теоретической части ОГЭ 2023 по информатике

В работе представлены 10 заданий с ответами решения варианта диагностического тестирования теоретической части ОГЭ по информатике.

1. В кодировке Windows-1251 каждый символ кодируется 8 битами.
Вова написал текст (в нем нет лишних пробелов):

"Вздыхать и думать про себя:
Когда же черт возьмет тебя!"

Ученик вычеркнул из текста одно слово. Заодно он вычеркнул ставший лишним пробел - два пробела не должны идти подряд. При этом размер нового предложения в данной кодировке оказался на 7 байт меньше, чем размер исходного предложения. Напишите в ответе вычеркнутое слово.

Решение

1. Переводим 8 бит = 1 байт – в 1 символе.

7 : 1 = 7 – символов вычеркнул Вова.

3. 7 – 1 = 6 - символов в слове. (из общего количества символов убрали 1 пробел)

Ответ: думать.

2. Валя шифрует русские слова, записывая вместо каждой буквы ее код. Коды букв даны в таблице.

Некоторые кодовые цепочки можно расшифровать несколькими способами. Например, 00101001 может означать не только УРА, но и УАУ.

Даны три кодовые цепочки:
01001010
11110001
0100100101

Найдите среди них ту, которая имеет только одну расшифровку, и запишите в ответе расшифрованное слово.

Решение
Рассмотрим три последовательности и для каждой выполним расшифровку и наблюдаем, что для 2 цепочки расшифровка единственная.

Три последовательности

Ответ: Ода.

3. Напишите наименьшее натуральное число х, для которого ложно высказывание: (х ≥ 3) ИЛИ НЕ (х ≥ 2).

Решение

1. Сначала избавляемся от НЕ во втором условии: (х ≥ 3) ИЛИ (х < 2).
2. Применяем закон де Моргана для логических условий: т.е. чтобы все условие было ложно надо применить операцию отрицание (НЕ) для всего высказывания и получаем:
   (х < 3) И (х ≥2).
3. 3. Анализируя 1 скобку получаем х= 2; 1; 0; …, 2 скобка х=2; 3; 4; 5; …
4. Следовательно наименьшее х, которое подходит это 2.

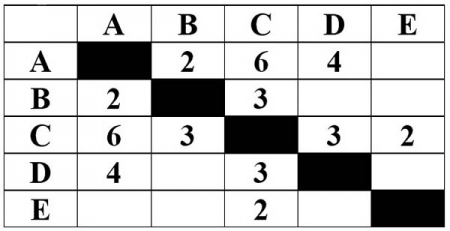
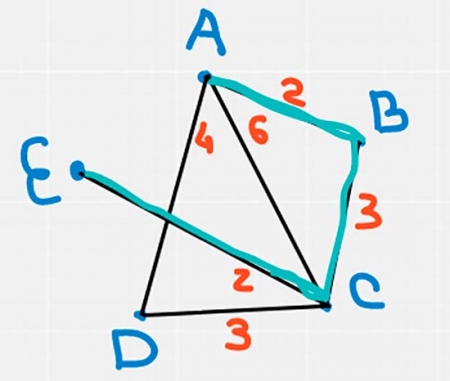
4. Между населенными пунктами А, В, С, D, Е построены протяженность которых (в километрах) приведена в таблице.

Таблица

Определите длину кратчайшего пути между пунктами А и Е. Передвигаться можно только по дорогам, протяженность которых указана в таблице. Каждый пункт можно посетить только один раз.

Решение
Так как необходимо найти длину кратчайшего пути из А в Е, то соответственно строим Пункты и соединяем дорогами из таблицы, так как, чтобы попасть в Е можно только через С, то ищем самый короткий маршрут из А в С, который является АВС=5 и прибавляем к нему расстояние из С в Е получаем: АВСЕ=7.

Решения задания 4

Ответ: 7.

5. У исполнителя Вычислитель две команды, которым присвоены номера:

1. вычесть 3.
2. приписать 1.

Первая из них уменьшает число на 3, а вторая приписывает к нему справа 1. Составьте алгоритм получения из числа 8 числа 15, содержащий не более 5 команд. В ответе запишите только номера команд. Если таких алгоритмов более одного, запишите любой из них.

Решение

1. Сначала из 8 – 3 = 5 (Команда 1)
2. Из 5 – 3 = 2 (Команда 1)
3. К 2 приписываем 1 = 21 (Команда 2)
4. Из 21 – 3  = 18 (Команда 1)
5. Из 18 – 3 = 15 (Команда 1) и выписываем номера команд в ответ

Ответ: 11211.

6. Ниже приведена программа, записанная на пяти языках программирования.
Python

Решение

1. Выписываем 9 запусков.
2. Проверяем сначала 2 условие t>11, соответственно 3 запуск печатает "YES" независимо от параметра "А"
3. Так как нам надо найти max значение "А" при котором программа напечатает "NO" 6 раз, то остается найти значение "А" при котором выведется еще 3 раза "YES", а это А=10, а это означает, что и при А=10 программа напечатает "NO" 6 раз.

Решение задания 6 ОГЭ

Ответ: 10.

7. Доступ к файлу ru.gif, находящемуся на сервере last.ru, осуществляется по протоколу https. Фрагменты адреса файла закодированы цифрами от 1 до 7. Запишите последовательность этих цифр, кодирующую адрес указанного файла в сети Интернет.

1. /
2. ://
3. last.
4. gif
5. https
6. ru.
7. ru

Решение:

1. Используя данные из текста, записываем полный путь к файлу
2. Используя расшифровку раскодируем и в ответе записываем последовательность цифр.

Путь к файлу

Ответ: 5237164

8. В языке запросов поискового сервера для обозначения логической операции "ИЛИ" используется символ "|", а для обозначения логической операции "И" - символ "&".
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

Какое количество страниц (в тысячах) будет найдено по запросу Скорпион | Козерог? Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Решение
Оформляем с помощью кругов Эйлера, составляем уравнения и находим неизвестный запрос.

Круги Эйлера

Ответ: 4400

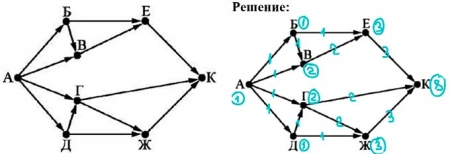
9. На рисунке - схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж и К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?

Схема дорог

Ответ: 8

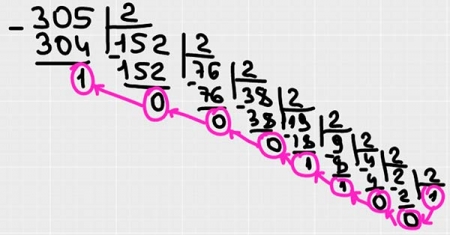
10. Переведите число 305 из десятичной системы счисления в двоичную систему счисления. Сколько единиц содержит полученное число? В ответе укажите одно число - количество единиц.

Решение

Переведем 305 из 10-й системы счисления в 2-ую используя, деление уголком.

Перевод числа в двоичную систему

Полученные остатки и последнее неполное частное записываем в обратном порядке – 100110001, в ответе записываем количество единиц в данном числе.
Ответ: 4