Информационный проект "Способы решения задач с параметром"

Проблема: данные задачи не разбираются в школе, так как их нет в курсе школьной программы. При этом присутствуют на едином государственном экзамене по математике

Цель: изучить способы решения задач с параметром и создать информационный плакат для учащихся 10-11 классов.

Противоречие: ученики хотят получить максимальный бал по профильному экзамену по математике, но при этом не умеют решать задачи такого типа.

Задачи проекта:

• изучить теорию по данному вопросу;
• ознакомиться со всеми способами решения таких задач;
• проработать дальнейший план работы над проектом с куратором;
• создать информационный плакат расписав схему решения.

Продукт: информационный плакат со схемами решения задач с параметром.

Введение

В курсе школьной программе уроков математики 10-11 классов данная тема не запланирована. Мы изучаем элементы на факультативных занятиях. Но во второй части профильного экзамена такое задание присутствует, при этом дает возможность получить ученику при правильном решении 4 балла.

Для начала разберемся, что же такое параметр?

В толковом словаре дается такое определение: "Параметр - это величина, характеризующая какое-нибудь основное свойство устройства, системы, явления или процесса".

В математике термин "параметр" используется в двух значения:

• величина, неизменная в данной задаче;
• вспомогательная переменная, не входящая в условие задачи, но удобная для решения или для наглядности.

А в чем же тогда особенность данных задач?

Каждая задача с параметрами представляет собой целый класс обычных задач, для каждой из которых должно быть получено решение.
Если в уравнении (неравенстве) некоторые коэффициенты заданы не конкретными числовыми значениями, а обозначены буквами, то они называются параметрами, а уравнение (неравенство) параметрическим.

Параметры обозначаются первыми буквами латинского алфавита: a, b, c, d, …, k, l, m, n, а неизвестные – буквами x, y, z. Решением неравенства (уравнения) с параметром является ответ в котором указано при каких значениях параметра будут существовать решения и каковы они будут.

Два уравнения (неравенства), содержащие одни и те же параметры, называются равносильными, если:

• если при одних и тех же значениях параметров оба выражения имеют смысл;
• баждое решение первого уравнения (неравенства) является решением второго и наоборот.

Актуальность

Задача с параметром – это одна из самых сложных задач предложенных на ЕГЭ. Такие задачи не рассматриваются в школе, но несмотря на это, знание набора методов и подходов к решению таких задач и определенная практика их решения позволят ученику если уж не решить ее полностью, то хотя бы приступить к ее решению и получить несколько баллов на ЕГЭ.

Теоретическая часть

Мы уже поняли, что такое параметр, и что из себя представляет задача с ним. Но что нам необходимо знать для их решения?

• Во-первых, нужно уметь правильно преобразовывать уравнения, неравенства и их системы.
• Во-вторых, детально изучить схему исследования квадратичной функции.

Какие же существуют основные методы для решения задач с параметром?

I способ

Сперва рассмотрим аналитический способ. Он используется для решения стандартных уравнений(неравенств) без параметра, но он не так уж и прост как на первый взгляд может показаться. Для использования данного способа вам необходимо знать большой объем математической информации и уметь грамотно это применять.

Идея: поскольку параметр считаем заданным числом, то решаем задачу по алгоритму, соответствующему данному типу уравнения: линейному, квадратному, иррациональному, тригонометрическому и т. д. При этом на каждом шаге алгоритма обращаем внимание на особенности: возможное деление на ноль, смену знака неравенства, извлечение корней, раскрытие модуля и т. п. Значения параметра, при которых возникают эти особенности, рассматриваем отдельно.

Пример решения:

Найдите все значения a, при каждом из которых уравнение |2x²+a+x+4|=|x²+2ax+2| имеет более одного корня

Решение:
Для начала преобразуем уравнение:
a(x²-6x+9)-2a=√(-2+(X-3)² ) <=> a(x-3)²-2a=√(x-3)²-2

затем сделаем замену переменных: пусть t=(x-3)², тогда a(t-2)=√(t-2)
Теперь пропишем условие: при замене t=(x-3)² для каждого положительного t найдется два различных значения x. Так как первая часть уравнения определена при t≥2, то это уравнение должно иметь ровно один корень t≥2. Сделаем еще одну замену, пусть y=√(t-2), тогда

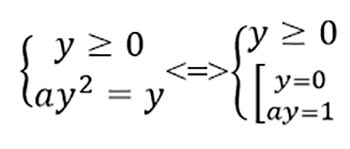
При замене y=√(t-2) для каждого y≥0 существует одно t≥2.Следовательно, последняя система должна иметь ровно один неотрицательный корень y. Так как y=0 уже является решением этой системы при любом a, то уравнение ay=1 не должно иметь неотрицательных решений. Это будет либо при a=0(в этом случае вообще нет корней), либо при a<0( в этом случае будет отрицательный корень). Из этого следует, что a∈(-∞├ 0].

Ответ: a∈(-∞ 0]

II способ

Другой метод - графический. Основная мысль данного метода в том, что в зависимости от задачи (с переменной x и параметром a) рассматриваются графики или в координатной плоскости (x; y), или в координатной плоскости (x; a). Сложность этого способа в том, что вам необходимо уметь четко и правильно строить графики, знать их свойства, а также уметь анализировать их.

Пример решения:
Найти все положительные значения a, при каждом из которых система уравнений имеет ровно три различных решения.

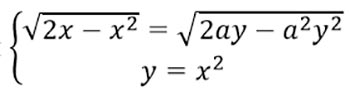
Для начала возведем в квадрат первое уравнение и добавим 1 к обеим его частям.

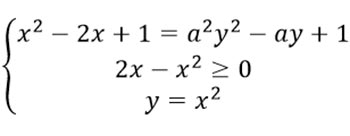
Ррешим второе выражение методом интервалов и получим отрезок, которому принадлежит x.

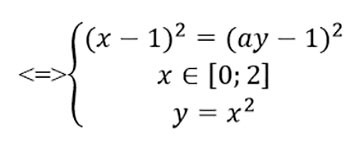
В первом выражении перенесем все в одну сторону и распишем разность квадратов.

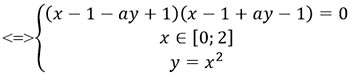
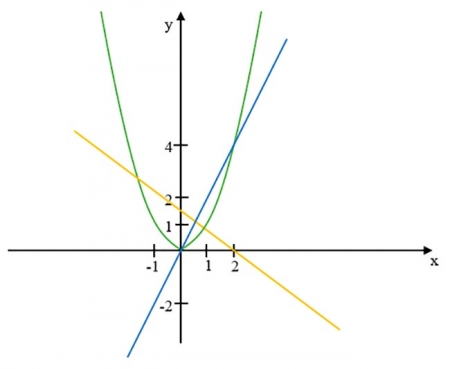
Условие 2ay-a²y²≥0 в систему можно не включать, так как оно следует из 2x-x²≥0 и 2x-x²=2ay-a²y². Следующим шагом построим графики:

Графики

Первому уравнению системы удовлетворяют пары (x;y), подходящие в уравнения y=x/a и y=-x/a+2/a (по условию a>0). Причем, y=x/a - это все прямые, проходящие через начало координат и образующие острый (ненулевой) угол с положительным направлением оси OX(так как a>0). (синий график)

Y=-x/a+2/a - это все прямые, проходящие через точку (2;0) и образующие тупой (ненулевой развернутый) угол с положительным направлением оси OX (так как a>0, то -1/a<0) (желтый график).

Решение данной системы — это точки пересечения параболы y=x² и этих прямых, при условии x∈[0;2]. Прямая y=x/a один раз пересекает параболу в точке (0;0) — это и решение, и второй раз, если прямая совпадает или расположена ниже прямой y=x/a, проходящей через точку (2;4). Эта прямая получается при 4=2/a <=> a=0,5 <=> 1/a=2. Таким образом, прямая y=x/a будет второй раз пересекать параболу для x∈[0;2] при 1/a≤2  a≥0,5.

Следовательно, при a∈[0,5;+∞)┤, за исключением того случая, когда прямые y=x/a и y=-x/a+2/a пересекают параболу в одной и той же точке, это происходит при:

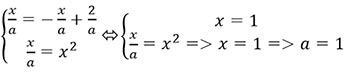
Тогда мы получаем ответ a∈[0,5;1)∪(1;+∞)

Ответ: [0,5;1)∪(1;+∞)

Квадратные уравнения и неравенства
Расположение корней квадратного трехчлена в зависимости от параметра.
Во-первых, вспомним, что выражение ax² +bx+c, где (a≠0), называется квадратичным трехчленом.
Функция f(x)=ax²+bx+c (a≠0), называется квадратичной.
Ее график получается параллельным переносом параболы y=ax², вершина которой сдвигается в некоторую точку.
Для того, чтобы найти координаты вершины параболы выделим полный квадрат:
ax²+bx+c=a(x²+b/ax)+c=a(x²+2b/2ax+(b/2a)²-(b/2a)²)+c=a(x+b/2a)²-b²/4a+c=a(x+b/2a)²-(b²-4ac)/4a
В числителе последней дроби появляется дискриминант D=b^2-4ac, следовательно:
F(x)=a(x+b/2a)²-D/4a

Смотря на второе выражение, мы видим, что координаты вершины параболы:
x₀=−b/2a ; y₀=−D/4a

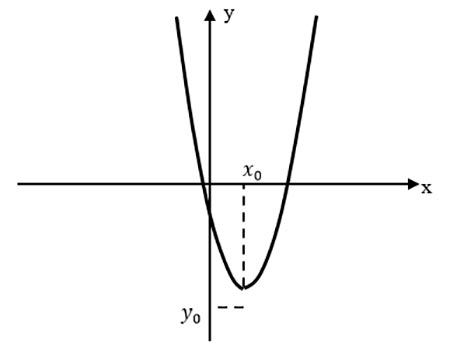
По нему мы наглядно видим, что при D>0 уравнение имеет два корня, вне зависимости от значения a. То есть для существования двух корней не важно, что ниже оси X лежит именно вершина параболы, значит вместо вершины можно взять любую другую точку. Таким образом, получается следующее утверждение: пусть f(x)=ax²+bx+c, a>0. Если для некоторого числа t выполнено неравенство f(t)<0, то квадратное уравнение ax²+bx+c=0 имеет два различных корня.

Основные утверждения по теме квадратные уравнения и неравенства

Утверждение № 1

Пусть f(x)=ax²+bx+c,a≠0. Для того, чтобы корни данного квадратного трехчлена лежали по разные стороны от некоторого числа t, необходимо и достаточно, чтобы выполнилось неравенство a∙f(t)<0.

Утверждение № 2

Пусть f(x)=ax²+bx+c,a≠0. Для того, чтобы корни данного квадратного трехчлена были больше некоторого числа t, необходимо и достаточно, чтобы выполнялась следующая система условий:

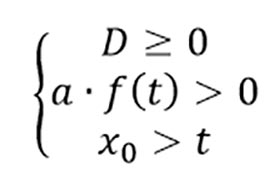
Аналогично для того, чтобы корни данного квадратного трехчлена были меньше некоторого числа t, необходимо и достаточно, чтобы выполнялась следующая система условий:

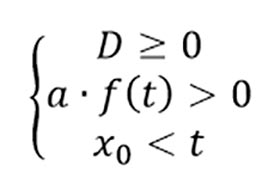
Утверждение 3

Пусть f(x)=〖ax〗^2+bx+c,a≠0. Для того, чтобы корни данного квадратного трехчлена принадлежали интервалу (s;t), необходимо и достаточно, чтобы выполнялась следующая система условий:

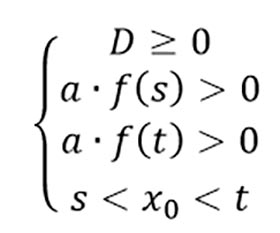
Утверждение 4

Пусть f(x)=ax²+bx+c,a≠0. Для того, чтобы отрезок [s;t] был расположен между корнями данного квадратного трехчлена, необходимо и достаточно, чтобы выполнялась следующая система условий:

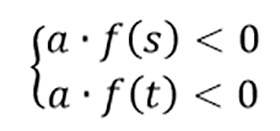
Основные утверждения в виде таблицы

Таблица

Пример анкеты (опрошено 37 человек)

1. В каком классе вы учитесь?
а) 9 класс.
б) 10 класс.
в) 11 класс.

2. Сдаете ли вы профильную математику на ЕГЭ?
а) Да.
б) Нет.

3. Знаете ли вы что такое задачи с параметром и как их решать?
а) Да знаю.
б) Знаю, что это такое, но не знаю как решать.
в) Нет.

4. Собираетесь ли поступать на бюджет?
а) Да.
б) Нет.

5. Проходили ли вы в школе или будете проходить задачи с параметром?
а) Да.
б) Нет.

6. Умеете ли вы решать неравенства с помощью графиков функции?
а) Да, они мне легко даются.
б) Да, но они у меня вызывают большие проблемы.
в) Нет, не умею.

7. Умеете ли вы решать неравенства с помощью уравнений?
а) Да, они мне легко даются.
б) Да, но они у меня вызывают большие проблемы.
в) Нет, не умею.

Практическая часть

Я провела опрос среди 9,10 и 11 классов, потому что для них данная тема является наиболее актуальной, в большинстве, опираясь на 10 классы. 

• Большинство учеников не знают, что такое задачи с параметром или не умеют их решать, а значит не способны решить 18 задачу из ЕГЭ.
• Большинство учеников собираются сдавать профильную математику, но при этом многие не умеют их решать.
• В большинстве школ не проходят данный тип задач, а значит ученикам придется готовятся к ним самостоятельно.

Ожидаемые эффекты

Социальный
Продукт проекта оказывает помощь для выпускников школ при сдачи ЕГЭ.
Финансовый
Увеличение возможности ученика 11 класса на получение наивысшего количества баллов при сдаче экзамена по математике, что способствует поступлению на бюджетный факультет, не требующий оплаты.

zadachi-s-parametrami.rar

Размер:

186.17 Kb

Скачали:

5