Алгоритм решения нелинейных уравнений методом сокращений отрезка локализации корня и шага вычисления функции

Предлагается авторский алгоритм нахождения корней нелинейных уравнений. В работе приводятся исследования эффективности алгоритма. Сравнительная оценка доказывает, что предлагаемый способ нахождения корней не уступает методу дихотомии или даже превосходит его.

Алгоритм можно использовать на практических занятиях в 9-11 классах при изучении программирования итерационных циклов.

Одним из основных методов нахождения корней нелинейных уравнений является метод деления отрезка пополам (дихотомии). Основным преимуществом этого метода является простота и высокая скорость сходимости. Благодаря этим достоинствам метод дихотомии имеет самое широкое применение на практике. Этот метод часто используется в школьной работе и доступен для понимания ученику из-за своей исключительной простоты.

Часто на уроках информатики педагоги используют этот алгоритм как один из примеров разработки итерационных циклических программ. Обычно школьникам объясняют идею алгоритма дихотомии, а затем разрабатывают программные модели решения нелинейных уравнений.

После того, как будет создана программа, можно посвятить часть учебного времени на проведение исследований, сравнив результаты, полученные программным способом с результатами, в электронной таблице методом "Поиск решения" и "Подбор параметра".

Однако, если вы работаете с мотивированной аудиторией, то возможен, на мой взгляд, более продуктивный путь: подвести учеников к тому, чтобы они сами "изобрели" метод деления отрезка пополам. Необходимо выслушать предложения самих учеников и перевести дискуссию в русло поиска разрешения проблемы: имеются нелинейные уравнения, нужно найти корни, а вот аналитические формулы для нахождения корней отсутствуют. Как быть?

Одним из возможных подходов, который решает эту проблему, является способ, который мною был назван как "Алгоритм сокращений отрезка локализации корня и шага вычисления функции" (АСОЛК).

Описание алгоритма

Последовательно сокращаются границы отрезка в 2ⁱ раз, где i – нечетные натуральные числа, начиная с единицы. На каждом шаге итерации сокращается отрезок локализации корня и одновременно уменьшается во столько же раз шаг, с которым вычисляется функция. Именно такой подход позволяет получить высокую скорость сходимости. Вычисления производятся до тех пор, пока не будет достигнута заданная точность, т.е. |f(x)| ≤ ε.

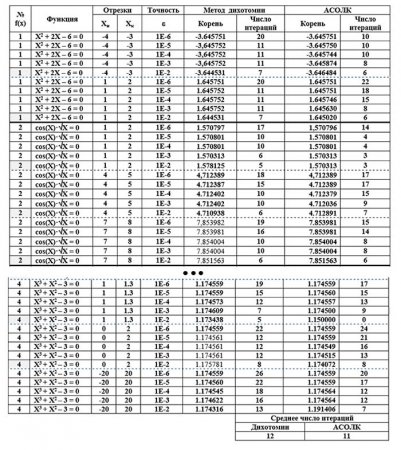
В таблице представлены результаты сравнительного анализа эффективности двух методов: Дихотомии и АСОЛК. Корни уравнений находились с точностью ε в диапазоне от 10^-2 до 10^-6.

С целью объективной сравнительной оценки способов, в таблице показаны результаты вычисления для четырех нелинейных уравнений на большой выборке исходных данных. Для определения скорости сходимости менялись начальные и конечные границы, в пределах которых локализуются корни уравнений.

В таблице представлено число итераций нахождения корней уравнений с заданной точностью, а также показано среднее число итераций для обоих методов на всем диапазоне данных, выбранных для исследования.

Выводы: среднее число итераций для дихотомии на этапе исследований составляет 12, АСОЛК – 11, что приблизительно одинаково. Тем не менее, способ АСОЛК несколько превосходит в эффективности метод дихотомии, что позволяет использовать его на практике наравне с методом дихотомии.

Нахождения корней уравнения с заданной точностью