Информационное моделирование в старшей школе. Численные методы нахождения корней нелинейных уравнений

На опыте практической работы показывается, как можно используя педагогические технологии, прежде всего такие как "Межпредметные связи", "Проектное и проблемное обучение" построить серию практических работ, развивающие творческие способности и исследовательские навыки учеников старшей школы.

В старших классах школы (10, 11 классы) совершенствуются навыки разработки и исследования информационных моделей, в том числе математических. Одним из заданий для школьников может быть разработка и исследование нахождения корней нелинейных уравнений, для которых отсутствуют, в отличие от квадратных, аналитические формулы нахождения корней. Именно на таких уроках школьник знакомится с численными методами нахождения корней.

Это позволит расширить кругозор учащихся, подготовить их к высшей школе, где эти вопросы изучаются более основательно. Кроме того, на таких работах можно совершенствовать приемы работы в табличном процессоре, а также навыки программирования. Ученик впервые узнает о численных методах приближенного вычисления корней с заданной точностью ε. Именно здесь уместно разобрать один из основных методов, а именно метод деления отрезка пополам (дихотомии), который применим для любой непрерывной функции, обладает высокой надежностью и скоростью сходимости.

Алгоритм нахождения корней методом деления отрезка пополам простой и доступен для понимания ученикам старшей школы. Кроме того, метод дихотомии имеет широкое применение и в других областях знаний и является мощным инструментом исследователя.

Для начала полезно разработать программную модель нахождения корней нелинейных уравнений на основе метода деления отрезка пополам, и только потом разрабатывать эту модель в электронной таблице. Такой подход позволит школьнику лучше понять используемые для этого надстройки "Поиск решения" и "Подбор параметра", применять эти средства не механически, а с пониманием их назначения и широких возможностей.

На мой взгляд, этот метод нужно изучать (объяснять) не сразу, а подвести их к осознанному выбору, позволяющему убедиться на практике в его эффективности, чтобы ученик почувствовал себя в роли первооткрывателя. Для этого надо поставить перед учеником проблему: как с помощью программных средств, не имея аналитической формулы "придумать" алгоритм решения этой задачи. Обычно ученики предлагают следующее:

1. Алгоритм должен быть циклическим.
2. Вычислять функцию с определенным шагом, который можно задавать при вводе данных.
3. Найти способ фиксации, когда значение функции меняет знак.
4. Значение корня должно быть найдено с определенной точностью с учетом того, что вычисления происходят с вещественными числами.
5. В качестве критерия эффективности способа выбрать число итераций, приводящих к нахождению корня с заданной точностью.

Для сокращения времени нахождения корней можно предложить сначала вычислять функцию с большим шагом, а когда найдена точка, когда функция меняет знак, отступить на шаг назад и теперь вычислять функцию со значительно меньшим интервалом.

Ученики убеждаются практически, что такой способ нахождения коней не эффективен, приводит к тому, что число итераций получается большим и вынуждает искать другие алгоритмы, которые ускорят процесс нахождения корней за меньшее число итераций. И только затем ученики изучаются метод дихотомии и разрабатывают программную модель.

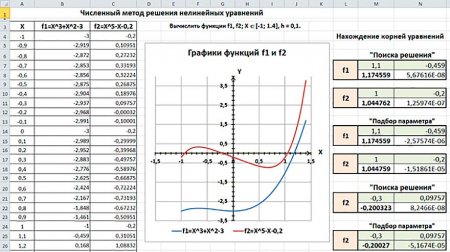
После этого разрабатывается модель в табличном процессоре, строятся графики функций, локализуются отрезки, где находятся корни уравнений, и после этого используются надстройки "Поиск решения", "Подбор параметра".

На заключительном этапе исследований обсуждаются методы решения нелинейных уравнений, сравниваются методы, преимущества и недостатки моделей, разработанные программным способом и с помощью табличного процессора.

Такой подход позволяет развить творческие способности и исследовательские навыки учеников, совершенствовать практические приемы программирования, работы с электронными таблицами.

Пример оформления модели в Excel представлен на рисунке.

Оформления модели в MS Excel