Графические методы решения алгебраических задач

Графический метод - это средство иллюстрации процессов, исчисления ряда показателей, оформление результатов анализа.

При правильном построении, графические средства обладают наглядностью, выразительностью, доступностью, способствующие анализу явлений, их обобщению и изучению.

Часто переход к графическому методу позволяет взглянуть на пример под другим углом и сфокусировать внимание на исследовании самой ее сути. Использование графического метода в решениях алгебраических задач – идея не новая и вместе с тем часто встречающаяся в ЕГЭ и вступительных испытаниях.

Однако мне и многим моим знакомым зачастую бывает сложно оценить задачу и догадаться до применения этого метода. В школе мы как правило концентрируемся на исследовании конкретных областей математики и уделяем недостаточно времени комбинированию этих областей и способов их работы друг с другом.

Именно стремлением доказать преимущества графического метода и вызвана моя научная работа.

Цель работы:

• на основе анализа теоретических материалов выделить и систематизировать основные графические методы, которые можно использовать в решении задач ЕГЭ;
• с помощью разбора соответствующих задач выделить и проиллюстрировать принципы, указывающие на целесообразность использования этих графических методов в решении;
• показать, как графический метод позволяет упростить решение задачи.

Задачи:

1. Изучить теоретические основы графического метода решения задач.
2. Рассмотреть примеры решения задач графическим методом.
3. Определить область применения графического метода решения задач.

Общие понятия о графическом и алгебраическом (аналитическом) методе

Черта между графическим и алгебраическом методами проводится еще в 7 классе посредством разделения некогда общего предмета математики на алгебру и геометрию.

Алгебра изучает свойства чисел, учит решать уравнения и по сути является обобщением и усложнением арифметики; геометрия же изучает пространственные отношения и формы.

Нетрудно понять, что

решить задачу алгебраическим (аналитическим) способом – значит решить ее посредством численных преобразований уравнений, а графическим – решить с помощью использования свойств геометрических фигур

При правильном построении, графические средства обладают наглядностью, выразительностью, доступностью, способствующие анализу явлений, их обобщению и изучению. Алгебраическое (аналитическое) решение часто выглядит более длинным, громоздким.

График на координатной плоскости

Простейшим переходом от алгебраического выражения f(x,у) к его графическому изображению является изображение функции f(x,у) на координатной прямой.
Функция – это соответствие вида y = f(x) между переменными величинами, в силу которого каждому рассматриваемому значению некоторой переменной величины x (аргумента или независимой переменной) соответствует определенное значение другой переменной величины, y (зависимой переменной, иногда это значение просто называют значением функции).

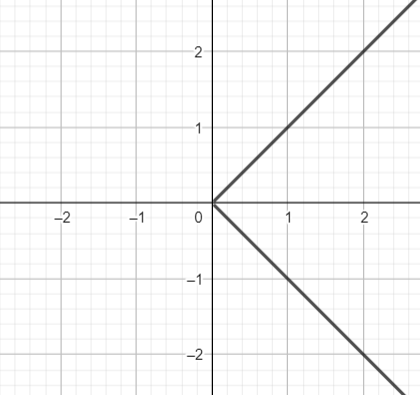
Заметим, что несмотря на то, что функция подразумевает, что одному значению аргумента х может соответствовать только одно значение зависимой переменной у, выражения, не соответствующие этому условию, так же могут быть изображены графически. Примером может служить выражение |y| = x (рис. 1)

Графиком уравнения с двумя переменными х и у, называется множество точек на ху-плоскости, координаты которых являются членами множества решений этого уравнения.

Для правильного построения графика и решения задачи необходимо знать свойства основных функций, методы их построения, а так же уметь выражать расстояния между прямыми и точками.

График прямой

• Линейной функцией называется функция вида y = kx + b.
• Прямую можно также представить в виде уравнения от двух переменных (х, у): ах + by + c = 0
• Коэффициент k отвечает за угол наклона прямой к оси Ox и равен его тангенсу: если k>0 то график наклонен вправо если k<0, то график наклонен влево.
• Коэффициент b отвечает за сдвиг графика по оси Oy
• Две прямые параллельны при равенстве коэффициентов k и неравенстве коэффициентов b; две прямые перпендикулярны, если произведение их коэффициентов k равно – 1 (k1*k2 = -1)

В графическом методе коэффициенты функций являются большим, чем просто числами задающими связь между х и у. Даже в линейной функции коэффициенты являются конкретными геометрическими параметрами – точкой и углом, что дает понять, как изменится ответ при их изменении. Это свойство необходимо понимать при решении задач с параметром, ведь именно там изменение числовых значений играет ключевую роль.

График квадратичной функции

• Параболой называется график функции y(х) = ax2+bx+c.
• Аналогично, старший коэффициент а влияет на ориентацию графика (ветви параболы направлены вверх при а>0 и вниз при а<0), а свободный член с – на сдвиг графика по оси 0y (парабола пересекает ось ординат именно в точке (0; с).
• Координата вершины параболы задается соотношением: х_{вершины} = (-b)/2a, y_{вершины} = у _{(х вершины)}

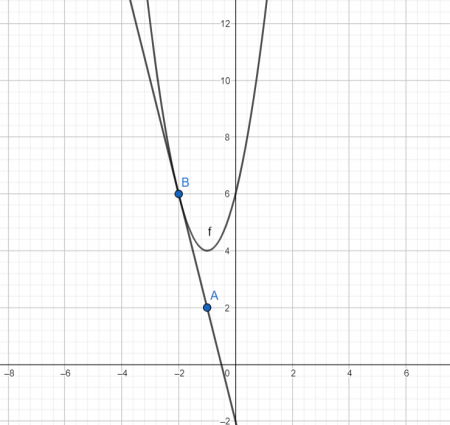
Во многих задачах требуется нахождение уравнения касательной к данной параболе, проведенной из данной точки (рис.2).

Касательная к параболе

Я предлагаю пользоваться следующим алгоритмом:

1. Из связи ya = kxa + b для точки А получаем первое уравнение системы
2. По определению, касательная – это прямая, имеющая с параболой только одну общую точку и не перпендикулярная её директрисе. Это значит, что уравнение kx + b = ax2+bx+c должно иметь только один корень. Тогда, приравнивая дискриминант получившегося уравнения к нулю, находим второе уравнение системы.

В приведенном примере мы воспользовались алгебраическим способом решения (использовали свойство квадратного уравнения), однако пришли к нему отталкиваясь от геометрических свойств касательной. В результате именно у нас получился синтез различных видов решений, встречающийся в подавляющем числе случаев.

Уравнение и график окружности

• Графиком уравнения (x – a)² + (y – b)² = r² является окружность на координатной плоскости хОу с центром в точке О’ (a; b) и радиусом r (r > 0).
• В частном случае при r = 0 уравнению будет соответствовать единственная точка плоскости (a; b)

Обратим внимание на особые свойства некоторых уравнений окружности при решении заданий с параметром a.

• Уравнение (x – a)² + (y – а)² = r² задает на координатной плоскости множество окружностей одинакового радиуса R с центром в точке (а; а) откуда следует, что y = x – это уравнение прямой, по которой «перемещается» центр окружности.
• Уравнение (x – a)² + (y - а²)² = r² задает на координатной плоскости множество окружностей одинакового радиуса R с центром в точке (а; а²) откуда следует, что y = x² – это уравнение параболы, по которой «перемещается» центр окружности.

Именно эти уравнения наиболее легко представляются графически и несут все свойства успешного графического решения, описанного в пункте 2.1.

Преобразование графиков функций

Чтобы построить график функции классическим методом нужно взять несколько точек и соединить их плавной линией. Однако этот прием требует большего количество времени в сравнении с построением графика при помощи некоторых геометрических преобразований.

Сжатие (растяжение) графика к (от) оси ординат (абсцисс):

Чтобы построить график функции f(kx), где k>1, нужно график функции f(x) сжать к оси Oy в k раз.

Тогда при 0< k < 1 график нужно растянуть ее от оси Oy в 1/k раз, при -1 ≤ k < 0 – отразить относительно оси Oy и растянуть ее в 1/k раз к ней, а при k<-1 – сжать отраженный график к оси Оу

Чтобы построить график функции k*f(x), где k>1, нужно график функции f(x) сжать к оси Ox в k раз. Действия при различных k аналогичны и для оси абсцисс, и для оси ординат.

Сдвиг графика влево/вправо вдоль оси абсцисс (параллельный перенос):

Чтобы построить график функции f(x+a), нужно график f(x) сдвинуть ВДОЛЬ оси Ox на a единиц влево;

Чтобы построить график функции f(x-a), нужно график f(x) сдвинуть ВДОЛЬ оси на a единиц вправо.

Сдвиг графика вверх/вниз вдоль оси ординат:

Чтобы построить график функции f(x)+b, нужно график f(x) сдвинуть ВДОЛЬ оси Oy на b единиц вверх;

Чтобы построить график функции f(x)-b, нужно график f(x) сдвинуть ВДОЛЬ оси Oy на b единиц вниз

Итак, чтобы построить график функции y = l*f(kx+a)+b нужно применить вышеуказанные правила сначала к аргументу, а затем к самой функции.

Графическое изображение неравенств (метод областей)

Метод областей является обобщением метода интервалов для выражений более высокой размерности. Для неравенства от одной переменной f(x) мы находили нули функции, отмечали их на числовой прямой (одномерное пространство) и выбирали числовые промежутки, в которых функция f(x) принимала нужный нам знак.

В неравенстве от двух переменных f(x, y) действия аналогичны: на координатной плоскости (двумерном пространстве) мы отмечаем все «нули», при которых f(x, y) = 0 (то есть сам график). Эти кривые разбивают плоскость на множества, в которых f(x, y) знакопостоянна.

Далее выбираем подмножества нужного нам знака (проверить знак подмножества можно с помощью подстановки соответствующих значений). Подходящие подмножества принято отмечать графически с помощью закрашивания.

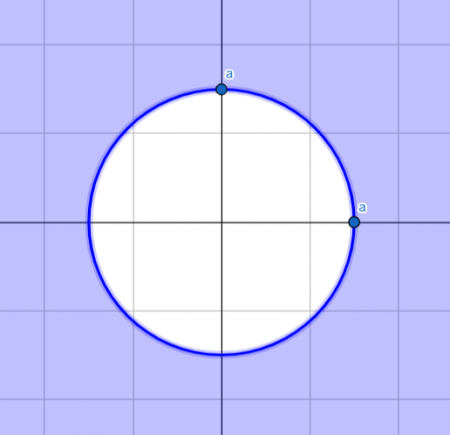
Например, решение неравенства x² + y² – a2 с помощью метода областей показано на рис.3.

Решение неравенства x2 + y2 &ndash; a2 с помощью метода областей

Окружность разбивает плоскость на два множества – внутри окружности и снаружи. Подстановка координат точки (0;0) дает отрицательный результат, значит решением будет область вне окружности.

Статья по математике на тему "Графические методы решения алгебраических задач" публикуется в сокращении. Скачать полную версию материала вы можете по ссылке ниже