Конспект внеклассного мероприятия "Занимательная математика"

Главная » Средние классы » Разное

Игра-соревнование "Занимательная математика" может быть проведена на занятии математического кружка или при проведении внеклассного мероприятия по математике.

Цель: создание условий для проявления индивидуальных творческих способностей учащихся, активизации их познавательной деятельности.

Планируемые результаты:

ознакомить учащихся с некоторыми видами олимпиадных задач по темам "Числовые закономерности", "Числа", "Геометрические конструкции";
формирование критичности мышления, развитию интуиции, эрудиции, логического мышления, геометрического воображения;
формировать умение работать в группе.

Ход занятия

Организационный этап

Ребятам предлагается объединиться в группы по цвету полученных карточек. Каждой группе предлагается распределить роли между собой и выполнять их при выполнении групповой работы.

Мотивационный этап

- Эпиграфом к занятию я выбрала высказывание Блеза Паскаля "Предмет математики настолько серьезен, что полезно не упускать случая, сделать его немного занимательным".
- Занятие проведем в виде командного соревнования. Путешествуя по миру "Занимательной математики", остановимся на станциях.

Станция "Числовые закономерности"

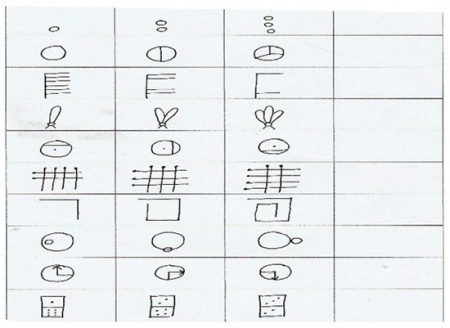
Задание 1. Определите закономерность и нарисуйте четвертую фигуру. Время выполнения: 3 минуты. За каждое правильно выполненное задание – 1 балл.

Определите закономерность и нарисуйте недостающую фигуру

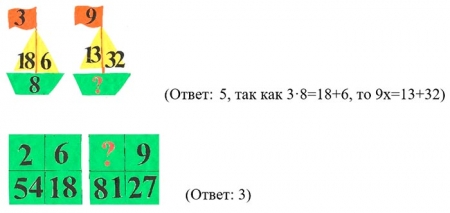
Задание 2. Вставьте недостающее число.

Вставьте недостающее число

Станция "Числа"

Задание 3. Число 30 легко выразить тремя пятерками 5·5+5. Попробуйте выразить 30 тремя другими одинаковыми цифрами. Результат работы оформите на листе бумаги. Время выполнения задания 5 минут. Каждый предложенный вами вариант - 1 балл.

Возможные ответы: 6·6-6=30; 3³+3=30; 33-3=30.

Задание 4. Какое наименьшее целое положительное число можно записать двумя цифрами? (2 балла)

Это не 10, а единица выраженная таким образом 1\1, 2\2, 3\3, …, 1º, 2º,…

Задание 5. Выразите 10 пятью девятками. Результат работы оформите на листе бумаги. Время выполнения задания 5 минут. Каждый предложенный вами вариант - 1 балл.

В случае затруднения ребятам предлагается ответить на вопросы-подсказки:

- Продолжите: 10 – это 9 и …
- Запишите 1 разными способами.

Возможные ответы: 9+99\99=10; 99\9-9\9=10, (9 9\9)9\9=10

Станция "Геометрические конструкции"

Задание 6. Можно ли из прямоугольника 16ˣ9 путем разрезания по сторонам клеток составить квадрат? Если да, то рассмотреть возможные варианты. (3 балла за доказательство без получения подсказки и по 1 баллу за каждый вариант разрезания)

В случае затруднения предлагается найти площадь данного прямоугольника и сделать вывод. Команды получают прямоугольники 16ˣ9, ножницы для наглядной демонстрации возможных вариантов разрезания.

Ответ: можно, так как 16ˣ9=144=12²

Задание 7. Квадрат разрезан на 4 равных треугольника. Какие выпуклые многоугольники могут быть сложены из этих треугольников? Результат работы оформите на листе бумаги. Время выполнения задания 5 минут. Каждый предложенный вами вариант - 1 балл.

Задание 8. Квадрат 4ˣ4 содержит 16 клеток. Найти как можно больше способов разрезания на 4 равные по площади части так, чтобы линия разреза шла по стороне клеток.
Результат работы оформите на листе бумаги. Время выполнения задания 5 минут. Каждый предложенный вами вариант - 1 балл.

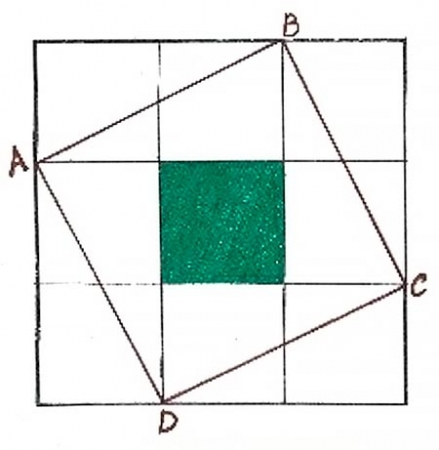
Задание 9. Площадь заштрихованной фигуры 5 см². Найти площадь четырехугольника АВСД.

Найди площадь четырёхугольника ABCD