Разработка урока по математике 6 класс "Модуль числа"

Цели урока:

• формирование понятия "модуль", умения находить модуль положительного и отрицательного числа.
• способствовать созданию творческой математической атмосферы;
• способствовать созданию творческой атмосферы урока, мотивировать учащихся точно и грамотно излагать свои мысли.

Предметные результаты:

• формирование научного типа мышления, научного представления о модуле числа, модуле произвольного числа, значении выражений, содержащих модули;
• владение научной терминологией, ключевыми понятиями темы: изображение чисел на координатной прямой.

Учебник: "Математика" 6 класс / С.М. Никольский, М.К. Потапов, Н.Н. Решетников. − М.: Просвещение, 2016.

Оборудование: аппаратура для показа презентации, квадрат с числами для устного счета, табличка с опорными словами для постановки цели занятия, ватман с незаполненной блок-схемой, теннисная ракетка и шарик для математического пинг-понга, ромашки Блума для каждого ученика, карточки с условиями для разно-уровневой самостоятельной работы.

Ход занятия

Оргмомент

Приветствие детей. Знакомство с эпиграфом урока.

Актуализация опорных знаний

Учитель: Ребята! Мы продолжаем путешествовать по стране целых чисел, в которую ученики младших классов не допускаются.
- А вы, дорогие шестиклассники, уже знакомы с координатной прямой, с помощью которой можете попасть в эту страну.
- Какая прямая называется координатной?

- Из чего состоит ряд целых чисел?
- Приведите примеры противоположных целых чисел.
- Нарисуйте квадрат состороной 3 см. Разделите его на 9 равных частей. Посмотрите на мой квадрат:

- В какой зависимости расположены числа? (Четные противоположные числа и нуль)
- Восстановите эти числа в своих квадратиках. Выполните самопроверку.

- Посмотрите на слайд.

- Какими числами заполнить пробелы? Как мы называем такие числа? (Противоположными)

Проверка домашнего задания

- Ребята, сегодня у нас в гостях Мистер Модуль!
- Давайте прочитаем, с какими словами он к нам обращается. Проверим домашнее задание и посмотрим, что вы уже знаете про модуль.

Учитель пишет в центре доски слово "Модуль". Обучающиеся выходят к доске попарно, прикрепляют подготовленные дома картинки: "Модуль в медицине", "Модуль в образовании", "Модуль в физике", "Модуль в математике", "Модуль в кораблестроении", "Модуль в космонавтике", "Модуль в строительстве", "Модуль в архитектуре", "Модуль в искусстве", "Модуль в развивающих играх" и т.п., сопровождая это небольшими пояснениями.

- Как мы называем такую схему? (Кластер)
- Общими усилиями мы составили кластер "Модуль" и рассмотрели сферы применения модулей. А можно еще расширить эту схему?
- Приведите примеры предметов, окружающих нас и состоящих из модулей. (модульное оригами, обшивка стен из полосок краноспана, полосы жалюзи и т.п.)

- От какого слова происходит слово "модуль"?

modulus от латин.- величина, маленькая мера

- Как вы думаете, на каком пункте кластера мы остановимся сегодня подробнее? ("Модуль в математике")
- Давайте по опорным словам "Наша цель", "повторить", "узнать", "научиться применять", "метацель" сформулируем цель нашего занятия.

• Повторить: определение координатной прямой, ряда целых чисел, противоположных чисел…;
• Узнать: определение модуля числа, кто впервые ввел, как обозначается…;
• Научиться применять: при решении упражнений; метацель: схематизировать новую информацию, составлять алгоритмы, работать, сотрудничая в коллективе.

Формирование новых знаний

- Итак, запишем тему занятия "Модуль числа".
- Термин "модуль числа" впервые ввел французский математик Жорж Аргон в 1806 году.
- Нарисуем координатную прямую. Обозначим на ней точки А(-5) и В(3). На каком расстоянии от начала координат расположены эти точки?

- Записывают это так: |-5|=5, |3|=3. Читают: минус пять по модулю равно пяти, три по модулю равно трем.
- Как вы думаете, что называется модулем числа? (это расстояние)
- Итак, модуль числа а - это расстояние от начала координат до точки с координатой а.

Запишем:|1| = 1, |36| = 36, |-4| = 4, |-9| = 9, |0| = 0.
- Решим устно № 217. Запишем № 218 с комментированием.
- Молодцы!

Физкультминутка "Математический пинг-понг"

- А теперь давайте все встанем. (Учитель имитирует подачу шарика ракеткой, задавая вопросы на повторение. Обучающиеся ладошкой показывают, кто может отбить шарик и ответить на вопрос)

Вопросы:

• Что называется масштабом?
• Что называется пропорцией?
• Какое основное свойство пропорции?
• Какие величины называются прямопропорциональными?
• Какие величины называются обратнопропорциональными?
• Что называется процентом?
• Что называется промилле?
• Что называется координатной прямой?
• Что называется модулем числа?

Закрепление нового материала

Учитель: Итак, какую тему мы рассматриваем? Что называется модулем числа а?

Если a > 0, то |a| = a
Если a = 0, то |a| = 0
Если a < 0, то |a| = -a

- Получим алгоритм определения модуля числа а.

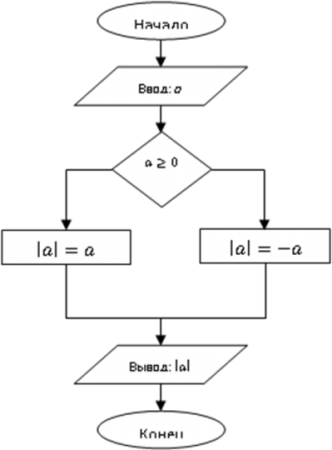
- А теперь давайте заполним блок-схему алгоритма. (дети сами заполняют предложенную блок-схему)

- Давайте "пропустим" несколько чисел через нашу блок-схему (a=5; a=-7; a=0). Правильно ли она работает?

Блок-схема

- Давайте обратимся к учебнику и решим: № 222 (у доски), № 224 (в парах с последующей проверкой).

Физкультминутка

- Встанем, немного расслабимся, представим, что сейчас лето, шуршат на деревьях листики (растирают ладоши), капают капельки (щелкают пальцами), дождик становится все сильнее (хлопают в ладоши), ливень (топают ногами).
- А теперь движения на координацию: одной рукой "пилим", другой - "забиваем".

- Одной рукой в воздухе рисуем цифру "5", другой - "2".
- Одной рукой в воздухе рисуем цифру "6", другой - букву "А".

Подведение итогов

- Итак, подведем итоги нашей работы. Ответим на вопросы по теме "Модуль числа".

• Что называется модулем числа а?
• Чему равен модуль положительного числа?
• Чему равен модуль отрицательного числа?
• Чему равен модуль нуля?
• Может ли модуль любого числа быть отрицательным?
• Чему равны модули противоположных чисел?

- Достигли ли мы поставленной цели?
- Давайте скажем "до свидания" нашему гостю - Мистеру Модулю. Мы с ним теперь будем часто встречаться на уроках математики.

Рефлексия

- А теперь заполним ромашку Блума.
- Ответьте, пожалуйста, на вопросы, записанные на ее лепестках (у каждого своя ромашка):

• Что узнали?
• Что хотелось бы уточнить?
• Где используется?
• Что понравилось / не понравилось?
• Как взаимодействовал класс?
• Какой возник ассоциативный образ для модуля числа?

- Давайте прикрепим наши ромашки на доску. (дети поочередно озвучивают некоторые свои ответы, магнитиками прикрепляя свой цветок, где также записана их самооценка)

Заключение

- Великий советский математик А.Н. Колмогоров сказал, что без занятия математикой нельзя понять ни основ современной техники, ни того, как ученые изучают природные и социальные явления.

- А мы сегодня убедились, что и математику необходимо изучать, применяя другие науки. Например, литературу (создание ассоциативного образа модуля числа), информатику (работа с блок-схемой, поиск информации в интернете), ИЗО (использование элементов модульного оригами, модульных картин при составлении кластера), психологию (при заполнении ромашки Блума), валеологию (во время физкультминутки).

Самостоятельная работа по теме "Модуль числа"

Самостоятельная работа с упражнениями по нарастающей сложности (с учетом, что дети сидят по одному):

1. Найти модули чисел: 8, -13, -15, 0, 83, -28, 72.

2. Запишите числа, модули которых равны 3, 0, 10, -91, -34, 51.

3. Найти разность: |5| - |-5|, |-6| - |6|, |-13| - |13|.

4. Заполните таблицу:

5. Найти значения выражений: |-12|+|45|; |-64|:|2|; |-69|*|23|+|-10|

6. Запишите числа в порядке возрастания их модулей: 83, -38, 10, 59, 0, 100, -23

7. Вычислите: (|-38|*|-26|)/(|-13|*|19|)

Домашняя работа

1. Выучить по учебнику п. 2.2.
2. Решить № 223, 225.
3. Решить дополнительно задания творческого характера № 228, 231.