Конспект урока математики в 6 классе: Прямая пропорциональность и ее график

Цель: знакомство с прямой пропорциональностью и построением ее графика.

Задачи:

• способствовать развитию наблюдательности, умению анализировать, обобщать, делать выводы;
• побуждать учеников к самоконтролю и взаимоконтролю;
• формировать навыки грамотного построения графиков.

Оборудование: компьютер, презентация, карточки с заданиями на каждого.

Ход урока

Организационный момент

- Доброе утро, ребята! Мне бы хотелось начать урок со следующих слов. Французский писатель Анатоль Франс (1844 – 1924) однажды заметил: "Учиться можно только весело. Чтобы переварить знания, надо поглощать их с аппетитом".
- Давайте следовать совету писателя. Будем активны, внимательны, будем поглощать знания с большим желанием, ведь они пригодятся вам в дальнейшей жизни.

Мотивация

- Возьмите карточки с математическими терминами, которые мы будем употреблять на уроке. Исправьте ошибки, допущенные в написании этих терминов.
- Поменяйтесь, листочками и проверьте, все ли ошибки исправлены.
- Что вы заметили? В каком слове нет ошибок? (функция)

Актуализация знания

- С понятием "функция" мы познакомились на предыдущих уроках. Давайте вспомним основные понятия и определения по этой теме. Что называется функцией? (Зависимость одной переменной от другой называют функциональной зависимостью или функцией)
- Как иначе называют независимую переменную? (агрумент)
- Зависимую переменную? (функцией этого аргумента)

- Что понимают под областью определения функции? (все значения, которые принимает независимая переменная)
- Что понимают под областью значения функции? (все значения зависимой переменной)
- Что называется графиком функции? (множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции)

В тетрадях записать число. Составьте формулы, для решения следующих задач. Путь S км, пройденный автомобилем за t ч, с постоянной скоростью 70 км/ч. вычисляется по формуле… Стоимость p товара в рублях по цене 15 р. за килограмм вычисляется по формуле…

- Какие переменные зависимые, независимые? Что от чего зависит? Какая зависимость?

Изучение нового материала

Введение понятия пропорциональные переменные

Цена яблок 36 руб. за кг. Если обозначить массу купленных яблок (в кг) буквой m, а их стоимость (в руб.) буквой s, то зависимость между этими переменными выражается формулой s = 36m.

Если взять два любых значения переменной s (например, 54 или 108) и соответствующие им значения переменной m (1,5 и 3), то составленная из них пропорция будет верной: 54/1,5 = 108/3 = 36.

Если любые две пары соответствующих друг другу значений зависимой и независимой переменных составляют верную пропорцию, то такие переменные называют пропорциональными, а их отношение называют коэффициентом пропорциональности. В рассмотренном примере коэффициент пропорциональности равен 36.

Пропорциональные переменные

Пропорциональными являются время движения с постоянной скоростью и пройденный путь, длина стороны квадрата и его периметр, масса однородного тела и его объем и т.п. Непропорциональны рост человека и его возраст, длина стороны квадрата и его площадь, скорость движения и время, затраченное на преодоление заданного расстояния и др.

Пропорциональные переменные обладают важным свойством: если значение одной переменной увеличить или уменьшить в несколько раз, то значение другой переменной также увеличится (уменьшится) во столько же раз, например, 3/1,5 = 108/54 = 2.

Зависимость стоимости яблок от массы купленных яблок, является примером функции, которая задается формулой y=kx, где k - число, отличное от нуля. Такую функцию называют прямой пропорциональностью.

- Сегодня на уроке мы будем изучать функцию, которая называется прямой пропорциональностью.
- Чему бы вы хотели научиться? (строить график, и т.д.)

Прямой пропорциональностью называется функция, которую можно задать формулой у=кх, где х – независимая переменная, а к – некоторое число, неравное нулю.

График прямой пропорциональности

Функция прямой пропорциональности

Прямой пропорциональностью называется функция, которую можно задать формулой вида y = kx, где x – независимая переменная, а k – неравное нулю число.
Число k называют коэффициентом пропорциональности.

Например, функция y = x/5 является прямой пропорциональностью (здесь k = 1/5), а функция y = 3/x и y = 4x + 7 не являются прямыми пропорциональностями.
Выясним, что представляет собой график прямой пропорциональности. (стр. 66 - 67)

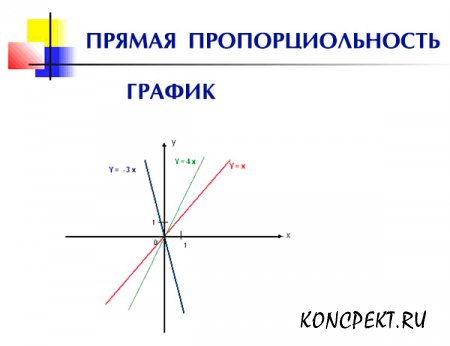
Вывод: График прямой пропорциональности представляет собой прямую, проходящую через начало координат. Чтобы построить график достаточно найти координаты какой-нибудь точки графика этой функции, отличной от начала координат, отметить эту точку и через нее и начало координат провести прямую.

Физкультминутка

Закрепление нового материала

№ 297
S=12t, является прямой пропорциональностью.

№ 299
y = -1/6 x , х = -9; 0; 1; 4
у = -1,5 0 -1/6 -2/3

№ 300
Постройте график прямой пропорциональности, заданной формулой…

Интерактивный модуль (контрольный), выполняет ученик с комментированием
Данный модуль состоит из 5 заданий. Задания направлены на усвоения понятий "прямая пропорциональность", "график прямой пропорциональности", а также умений: находить значение функции по заданному значению аргумента и наоборот, если функция задана формулой; определять принадлежность точек графику функции; устанавливать положение графика прямой пропорциональности в координатных четвертях; строить график прямой пропорциональности.

При решении заданий учащемуся предоставляется возможность использовать подсказки. Все задания данного учебного модуля параметризированы. Это позволяет формировать индивидуальные задания для каждого учащегося

Данный модуль состоит из 5 заданий. Задания направлены на усвоения понятий "прямая пропорциональность", "график прямой пропорциональности", а также умений: находить значение функции по заданному значению аргумента и наоборот, если функция задана формулой; определять принадлежность точек графику функции; устанавливать положение графика прямой пропорциональности в координатных четвертях; строить график прямой пропорциональности. При решении заданий учащемуся предоставляется возможность использовать подсказки. Все задания данного учебного модуля параметризированы. Это позволяет формировать индивидуальные задания для каждого учащегося.

Самостоятельная работа с самопроверкой

Подведение итогов

- Давайте еще раз вспомним, с какой функцией мы сегодня на уроке познакомились? (Прямая пропорциональность)
- Функция какого вида называется прямой пропорциональностью? (у = кх)
- Что представляет собой график прямой пропорциональности? (Прямая, проходящая через начало координат)
- Как построить график прямой пропорциональности? (Построить таблицу значений функции, одна из точек – начало координат, вторая точка выбирается произвольно)
- Как называется число k в формуле прямой пропорциональности? (Коэффициент пропорциональности)

Домашнее задание
П. 15, № 301, 308, 309