Изучение теории графов в школьном курсе информатики: задачи и методика

Цель: рассмотреть возможности применения теории графов в школьном курсе информатики и показать, как графовые модели помогают решать задачи и развивать логическое и алгоритмическое мышление у учащихся.

Задачи:

• проанализировать, как теория графов используется в учебных задачах по информатике;
• показать практические примеры решения графовых задач из школьных учебников 10–11 классов;
• рассмотреть методический потенциал графовых моделей для повышения эффективности обучения и развития ключевых компетенций школьников.

Актуальность темы и использование графов

Современный мир – это эпоха цифровых технологий. Сегодня IT-специалисты востребованы как никогда, а профессии в сфере информационных технологий считаются одними из самых перспективных. Это привело к росту интереса абитуриентов к направлениям, связанным с информатикой и программированием.

Развитие цифрового общества способствовало активному применению теории графов – раздела математики, который изначально использовался лишь для решения головоломок и игр.

Благодаря своей наглядности и универсальности, графы нашли применение в самых разных областях: от проектирования микросхем и анализа алгоритмов до биоинформатики, экономики, логистики и искусственного интеллекта.

Опрос учителей и учащихся по применению теории графов

Применяют ли учителя-предметники элементы теории графов в образовательных учреждениях при обучении математике и информатике? Знакомы ли учащиеся с теорией графов? Имеется ли понимание у учащихся, что теория графов является мощным средством моделирования?

Для исследования отношения к теории графов у всех участников учебного процесса был проведен опрос среди учителей и учащихся по всей России.

Опрос учителей показал, что основной причиной редкого использования теории графов на уроках информатики в основной школе является отсутствие эффективной методики обучения данной теме (45 %), отсутствие мотивации к обучению (25 %) и отсутствие времени на изучение (30 %).

Но большинство опрошенных учителей (порядка 75 %) считает, что изучение теории графов является необходимым, и они хотели бы углубить свои знания в этой области знаний.

Задачи школьного курса информатики в терминах графов

Цель данной статьи – рассмотреть основные задачи школьного курса информатики, сформулированные в терминах графов или для которых можно построить графовые модели.

Рассмотрим решение некоторых задач из учебников по информатике за 10, 11 классы Босовой Л.Л.

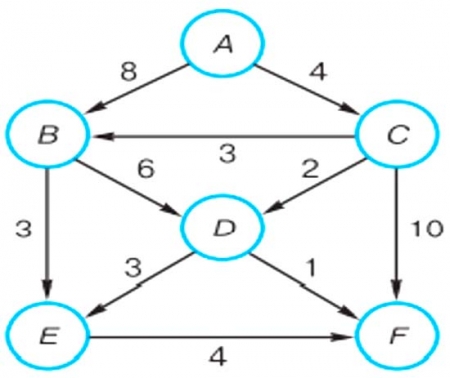
Задача 1. Найдите кратчайший путь из вершины A в вершину F в ориентированном графе:

Ориентированный граф

Решение задачи 1
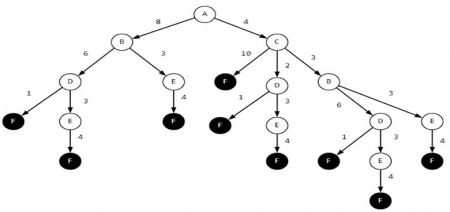
Данный граф – ориентированный граф с весом. "Расслоим" граф в дерево с корнем в вершине А и листьями в вершине F.

"Расслоим" граф в дерево

Выберем ветвь с наименьшим суммарным весом. Это и будет кратчайший маршрут из А в F.
Ответ: А-С-D-F.

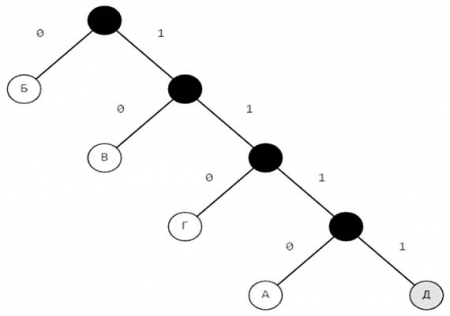
Задача 2. Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, используется неравномерный двоичный код, позволяющий однозначно декодировать полученную двоичную последовательность.

При этом используются следующие коды: А – 1110, Б – 0, В – 10, Г – 110. Каким кодовым словом может быть закодирована буква Д? Код должен удовлетворять свойству однозначного декодирования. Если можно использовать более одного кодового слова, укажите кратчайшее из них.

Решение задачи 2
Напомним свойство однозначного декодирования: никакое кодовое слово не является началом другого кодового слова. Для букв А, Б, В, Г кодовые слова известны. Нам остается лишь подобрать кодовые слова для буквы Д, которая будет удовлетворять свойству однозначного декодирования.

Для наглядности построим дерево, отметим на нем вершины, для которых известны кодовые слова.

Построим дерево

1, 11, 111 не являются ответами на вопрос задачи, поскольку не удовлетворяют свойству однозначного декодирования, т. е. нельзя "подвесить" буквы В, Г, А соответственно.

Из графа видим, что остался один "свободный" код – 1111. Соответственно, буква Д имеет кодовое слово 1111.

Ответ: 1111.

Задача 3. Во фрагменте базы данных представлены сведения о родственных отношениях:

Сколько внуков у Решко Д.А.?

Решение задачи 3
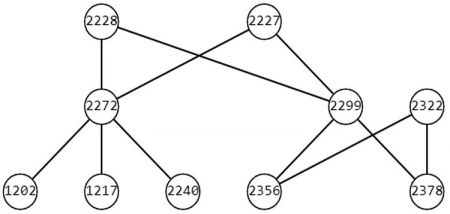
Построим граф, соответствующий заданной таблице 2. Вершинами графа будут идентификационные номера людей, а ребрами – родственные связи. Например, человек с ID 2227 является родителем 2272.

В конечном итоге получим следующий граф:

Граф для решения задачи 3

Далее будем анализировать полученный граф и таблицу 1. Решко Д.А. соответствует ID 2227. Из графа видим, что люди с идентификационными номерами 2272 и 2299 являются детьми Решко Д.А., следовательно, 1202 (Ландау М.А.), 1217 (Тесла П.А.), 2240 (Решко В.А.), 2356 (Диковец Т.И.), 2378 (Диковец П.И.) – внуки.

Ответ: 4.

Дидактический потенциал графовых моделей

Стоит отметить, что в современных школьных учебниках по информатике предлагаемые задачи, как правило, решаются без привлечения аппарата теории графов.

Между тем, графовые модели обладают значительным дидактическим потенциалом для разных возрастных групп учащихся. Благодаря своей наглядности и возможности подачи в игровой форме, элементы теории графов могут быть адаптированы даже для начальной школы.

Решение графовых задач способствует комплексному развитию у школьников: формированию логического и алгоритмического мышления; развитию навыков самостоятельной работы; стимулированию творческого подхода к решению задач.

Такой методический подход позволяет не только повысить эффективность обучения, но и сделать процесс освоения математических концепций более увлекательным для учащихся всех возрастов.