Решение Логико-алгоритмических задач на уроках информатики на примере задач на переливание

Логико-алгоритмическое мышление - это методы системного мышления, методы и соответствующие мыслительные операции, которые направлены на решение теоретических и практических задач, что в результате дает алгоритмы как специфические продукты человеческой деятельности.

Современный этап развития общества характеризуется внедрением информационных технологий во все сферы человеческой деятельности.

Новые информационные технологии оказывают существенное влияние и на сферу образования. Одной из дидактических задач образовательного учреждения является всестороннее формирование мышления учащегося, развитие его интеллекта. Важной составляющей интеллектуального развития человека является логико-алгоритмическое мышление.

Наибольшим потенциалом для формирования логико-алгоритмического мышления школьников среди естественнонаучных дисциплин обладает информатика. Анализ развития стандарта образования по информатике позволяет сделать вывод: формирование логико-алгоритмического мышления школьников - важная цель школьного образования на разных ступенях изучения информатики.

С каждым годом значительно возрастают требования к подготовке школьников и уровню развития их мышления. Учащиеся должны быстро принимать решения, составлять план действий в непредвиденной ситуации, моделировать и составлять абстрактные модели, сравнивать и обобщать объекты, самостоятельно решать сложные задачи и уметь искать информацию, которая поможет в решении тех или иных вопросах.

Можно выделить четыре уровня сформированности алгоритмической компетентности учащихся:

1. предметный,
2. атрибутивный,
3. логико- алгоритмический,
4. творческий.

На первом уровне – предметном – учащиеся осваивают работу по алгоритму, по предъявленному образцу без проведения анализа предлагаемых действий, правильности каждого шага данного алгоритма.

На атрибутивном уровне учащиеся уже проводят несложный анализ, связанный с рационализацией предложенного алгоритма, т.е. могут изменять последовательность действий/шагов, производить замену одних действий другими, исключать или добавлять действия.

Логико-алгоритмический уровень предполагает:

• умение самостоятельно составить алгоритм для решения стандартной задачи, выделить ряд задач, для которых применим этот алгоритм;
• понимание выбора алгоритма, его оптимального соответствия поставленной задаче;
• проведение обоснований выбора каждого шага/действия, последовательности шагов;
• умение указать на особенности применения данного алгоритма к каждой задаче выделенного круга.

Логико-алгоритмическое мышление определяется следующими компонентами:

1. Анализ требуемого результата и выбор на этой основе исходных данных для решения проблемы.
2. Выделение операций, необходимых для решения.
3. Выбор исполнителя, способного осуществлять данные операции.
4. Упорядочение операций и построение модели процесса решения.
5. Реализация процесса решения и соотнесение результатов с тем, что следовало получить.
6. Коррекция исходных данных или системы операций в случае несовпадения полученного результата с предполагаемым.

Примеры решения задач на переливание

В задачах на переливания, которые изучаются в курсе информатики начиная с 5 класса, требуется указать последовательность действий, при которой осуществляется требуемое переливание и выполнены все условия задачи.

Если не сказано ничего другого, считается, что

• все сосуды без делений;
• нельзя переливать жидкости "на глаз";
• невозможно ниоткуда добавлять жидкости и никуда сливать.

Мы можем точно сказать, сколько жидкости в сосуде, только в следующих случаях:

• знаем, что сосуд пуст;
• знаем, что сосуд полон, а в задаче дана его вместимость;
• в задаче дано, сколько жидкости в сосуде, а переливания с использованием этого сосуда не проводились;
• в переливании участвовали два сосуда, в каждом из которых известно, сколько было жидкости, и после переливания вся жидкость поместилась в один из них
• в переливании участвовали два сосуда, в каждом из которых известно, сколько было жидкости, известна вместимость того сосуда, в который переливали, и известно, что вся жидкость в него не поместилась. Мы можем найти, сколько ее осталось в другом сосуде.

Методики решения задач на переливание

Метод рассуждений. При решении чаще всего используются метод рассуждений. Этот способ является самым примитивным, с помощью которого решаются самые простые логические задачи. Его идея состоит в том, что учащиеся проводят рассуждения, используя последовательно все условия задачи, и приходят к выводу, который и будет являться ответом задачи.

Метод таблиц - основной прием, который используется при решении текстовых логических задач, заключается в построении таблиц. Таблицы не только позволяют наглядно представить условие задачи или ее ответ, но в значительной степени помогают делать правильные логические выводы в ходе решения задачи.

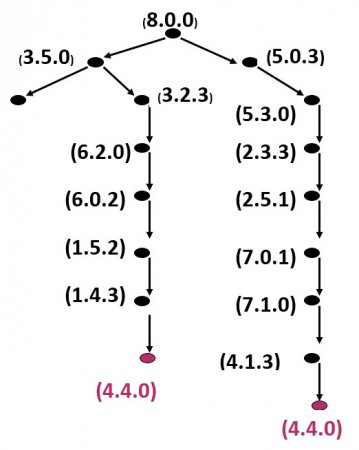
Метод граф. Решение задач на переливание с помощью графов, т.е. графических схем, состоящих из точек, соединенных между собой стрелками

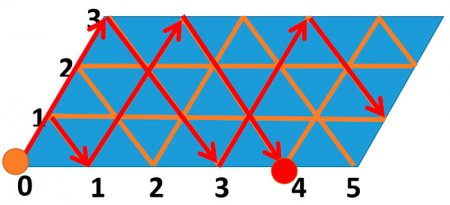
Метод бильярда. Для каждого случая предлагалось строится бильярдный стол из равносторонних треугольников, длины двух сторон которого численно равны объему двух меньших сосудов.

Далее, из острого угла этого стола вдоль одной из сторон нужно "запустить" шарик, который по закону "угол падения равен углу отражения" будет сталкиваться с бортами стола, показывая тем самым последовательность переливаний.

По уровню сложности можно выделить:

Задания 1 уровня - В 1 сосуд входит 8 л жидкости, во второй – 5 л, в третий – 3 л. Первый сосуд наполнен водой, а остальные два пусты.. Как с помощью этих сосудов отмерить 1 л воды?
Задание 2 уровня - Каким образом можно отмерить ровно 6 л воды, если имеются только два ведра: одно емкостью 4 л, другое – 9 л.
Задание 3 уровня. В бочке налито 18 л бензина. Имеются 2 ведра по 7 л, в которые нужно налить по 6 л бензина. Кроме того, есть черпак объемом 4 л. Как можно осуществить разлив?

Примеры решения задач разными методами

Решение рассуждением.

Задание 1. Выполняя лишь операции "наполним больший сосуд 8-0-0", "перельем из большего сосуда в меньший 0-5-3", "опорожним меньший сосуд 5-3-0", вновь перельем из большего сосуда в меньший 2-3-3", еще раз "опорожним меньший сосуд 2-5-1" получим последовательность: 8-0-0; 0-5-3; 5-3-0; 2-3-3; 2-5-1.

Решение путем составления таблицы.

Решение с помощью графов

Граф

Решения методом бильярда

Метод бильярда

Задача. Есть 2 ведра: 3 и 5 литров. Нужно получить 4 литра.

Задания для самостоятельного решения

Задача 1. Имеются один сосуд 12 л, который наполнен водой, и еще два пустых сосуда емкостью 5л и 8л. Как разделить воду на две равные части?
Задача 2. Бидон, емкость которого 10л, наполнен керосином. Имеются еще пустые сосуды в 7л и 2л. Как разлить керосин в два сосуда по 5л каждый?
Задача 3. Имеется сосуды вместимостью 12, 9 и 5 л. Первый из них наполнен некоторой жидкостью, а два остальных - пустые. Как разлить воду в два из этих сосудов так, чтобы в каждом было по 6 л?

В заключении можно сформулировать 2 правила, позволяющие судить о возможности решения конкретной задачи:

1. Пусть имеются два пустых сосуда объемом A литров и B литров и требуется набрать ровно C литров воды. Если число C не делится на наибольший общий делитель чисел A и B, то это сделать невозможно.
2. Если C делится на наибольший общий делитель чисел A и B, то в таком случае задача всегда имеет решение. В частности, это всегда возможно, если числа A и B взаимно просты.