Роль моделирования при решении арифметических задач в начальной школе

На современном этапе развития науки происходит повсеместная компьютеризация, которая предполагает высокий уровень владения не только техникой, но и грамотно сформированным математическим мышлением.

В ФГОС НО второго поколения в математической подготовке особое место отведено деятельностному, практическому содержанию образования.

А именно конкретным способам деятельности, применению приобретенных знаний и умений в реальных жизненных ситуациях (ФГОС НОО). С такими ситуациями дети знакомятся на примере решения арифметических задач.

В процессе развития математического образования в начальной школе обучение младших школьников решению арифметических задач было и остается одной из самых актуальных проблем. Умение решать арифметические задачи является определяющим показателем степени математического развития ребенка, глубины усвоения им математического материала.

В начальном курсе математики понятие "задача", как правило, употребляется тогда, когда речь идет о текстовых арифметических задачах. Они формулируются в виде текста, в котором находят отражение количественные отношения между реальными объектами. В методике используются различные трактовки понятия текстовая арифметическая задача.

Вслед за М. А. Бантовой под арифметической (текстовой) задачей мы будем понимать бесконечное множество таких жизненных ситуаций, которые связаны с числами и требуют выполнения арифметических действий над ними. Каждая задача включает число данные и искомые. Задача имеет условие и вопрос. В условии указываются связи между данными числами, а также между данными и искомым; эти связи и определяют выбор соответствующих арифметических действий. Вопрос указывает, какое число является искомым.

Решить задачу – значит выявить связи между данными и искомым, заданные условием задачи, на основе чего выбрать, а затем выполнить арифметические действия и дать ответ на вопрос задачи.

На начальной ступени школьного образования наибольшее количество затруднений учащиеся испытывают при решении тестовых задач. Это связано с возрастными особенностями школьников, с тем, что у них еще не развито абстрактное мышление. На первом этапе необходимо сформировать у младших школьников понятие текстовой задачи. В качестве критерия сформированности этого понятия принимается умение учащегося определять, является ли предложенный текст задачей или нет.

Научившись отличать задачу от обычного текста, учащиеся могут приступать к решению задач. Для этого многие учителя используют на своих уроках метод моделирования, который помогает ученику не только понять задачу, но и самому найти способ ее решения.

Изучением вопроса моделирования занимались такие видные ученые и педагоги, как Д.Б. Эльконин, В.В. Давыдов, Н.Г. Салмина, П.В. Трусова и другие. У каждого из них было свое понятие о модели и моделировании и каким образом можно использовать моделирование в школьном образовании.

Анализируя понятие "моделирование", используемое в педагогике, необходимо изначально дать определение термину "модель". По мнению С.А. Бешенкова, модель – это искусственно созданный объект в виде схемы, физических конструкций, знаковых форм или формул, который, будучи подобен исследуемому объекту (или явлению), отображает и воспроизводит в более простом виде структуру, свойства, взаимосвязи и отношения между элементами этого объекта. Благодаря моделям учащиеся могут визуально представить объекты, недоступные для непосредственного восприятия.

В работах А.И. Богатырева моделирование рассматривается как процесс создания, исследования и использования моделей. Формы моделирования разнообразны и зависят от используемых моделей и сферы их применения. По характеру моделей традиционно выделяется предметное и знаковое (информационное) моделирование.

Другими словами, модель – это физический или абстрактный объект, свойства которого в определенном смысле сходны со свойствами исследуемого объекта (рисунки, графики, модели и т.п.).

Моделирование – это процесс построения и изучения моделей, а методы моделирования – это методы, с помощью которых происходит процесс моделирования (анализ, синтез, обобщение и т.д.)

Таким образом, мы видим, что все эти понятия тесно взаимосвязаны между собой.

Основное внимание на начальном этапе обучения решению задач уделяется ознакомлению со структурой задачи, умению выделять числовые данные, устанавливать связи между ними, называть и выполнять арифметические действия сложения и вычитания. Решение таких задач происходит с опорой на восприятие конкретных множеств и не вызывает у детей трудностей. Но этот этап необходим, чтобы затем перейти к решению задач с использованием метода моделирования.

Учитель уделяет внимание не только умению учащихся выполнять математический анализ задач и выявлять связи между условием и вопросом, а также он учит школьников представлять эти связи в виде моделей.

Обучение моделированию занимает достаточно много времени в формировании умения решать задачи, так как именно оно способствует математическому развитию ребенка. Моделирование является общей деятельностью учителя и учащихся, которая предполагает замещение реальных предметов условными рисунками, схемами и т.д.

Необходимость овладения младшими школьниками методом моделирования как методом познания в процессе образования можно обосновать с разных позиций:

• это способствует формированию интереса к учебному предмету и образовательному процессу;
• как показывают эксперименты, введение в содержание обучения понятий модели и моделирования существенно меняет отношение учащихся к учебному предмету, делает их учебную деятельность более осмысленной и более продуктивной;
• целенаправленное и систематическое обучение методу моделирования приближает младших школьников к методам научного познания, обеспечивает их интеллектуальное развитие.

Для того чтобы "вооружить" учащихся моделированием как способом познания, учителю недостаточно лишь демонстрировать им разные научные модели и показывать процесс моделирования отдельных явлений. Нужно, чтобы школьники сами строили модели, сами изучали какие-либо объекты, явления с помощью моделирования.

Когда учащиеся, решая практическую математическую (сюжетную) задачу, понимают, что она представляет собой знаковую модель некоторой реальной ситуации, составляют последовательность различных ее моделей, затем изучают (решают) эти модели и, наконец, переводят полученное решение на язык исходной задачи, то тем самым школьники овладевают методом моделирования.

Метод математического моделирования позволяет научить школьников:

• анализу (на этапе восприятия задачи и выбора пути реализации решения);
• установлению взаимосвязей между объектами задачи, построению наиболее целесообразной схемы решения;
• интерпретации полученного решения для исходной задачи;
• составлению задач по готовым моделям и др.

Приведем несколько примеров задач, которые встречаются в учебниках начальной школы, и моделей, которые можно построить для решения данных задач. УМК "Начальная школа XXI века" 2 класс ч. 2: В.Н. Рудницкая.

Задача: Испекли 12 пирожков. Две трети всех пирожков съели. Сколько пирожков съели?

12 пирожков

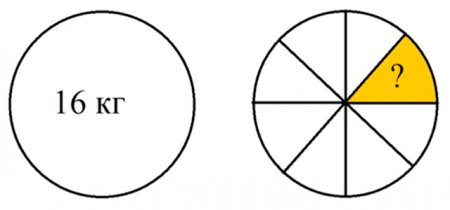
Задача: Масса тыквы 16 кг. Восьмую часть этой тыквы использовали для приготовления каши? Сколько килограммов использовали?

Масса тыквы

Использование моделирования как основного метода решения арифметических задач позволяет детям отделить главное от второстепенного, понять связи и отношения и как итог – научиться решать арифметические задачи различных типов.

Моделирование формирует у детей умение планировать свою деятельность, умение находить главное в окружающей его действительности, умение ставить перед собой цели и находить различные пути их решения. А это основная цель обучения.