Комбинаторные задачи. Методы решения

В настоящее время в учебных пособиях по теории вероятностей выделяют следующие основные методы решения комбинаторных задач: перебор всех возможных вариантов (систематический перебор, перебор с ограничениями), полный граф, дерево вариантов (граф-дерево), таблица вариантов, правила произведения и суммы.

Сами задачи подразделяют на следующие типы:

задачи, в которых требуется перечислить все решения;

задачи, состоящие в требовании выделить из всех возможных решений такое, которое удовлетворяет заданному дополнительному требованию;

задачи, в которых требуется подсчитать число решений.

Самые простейшие задачи, с которых начинается изучение комбинаторики, связаны с составлением различных комбинаций из трех элементов.

Примеры и методы решения комбинаторных задач

Пример 1

Три друга Антон, Борис и Виктор – приобрели два билета на футбольный матч. Сколько существует вариантов посещения футбольного матча для троих друзей?

Решение: По имеющимся двум билетам на матч могут пойти:

1. либо Антон и Виктор,
2. либо Антон и Виктор,
3. либо Борис и Виктор.

Ответ: три варианта.

Пример 2

Сколько различных трехзначных чисел можно записать с помощью цифр 1, 2, 3 при условии, что цифры в числе:

1. должны быть различными;
2. могут повторяться?

Решение: Ответ на первый вопрос получим аналогично решению из примера 1: 123, 213, 132, 312,231, 321. Получили 6 чисел.

Ответ на второй вопрос получим следующим образом. Выпишем все числа, начинающиеся с цифры 1 в порядке их возрастания; затем - начинающиеся с цифры 2; после чего - начинающиеся с цифры 3:

Получили 27 чисел. При подсчете числа комбинаций из двух элементов необходимо исключить возможность "потери" какой-либо комбинации. Для этого существует такое средство, как таблица вариантов.

Пример 3

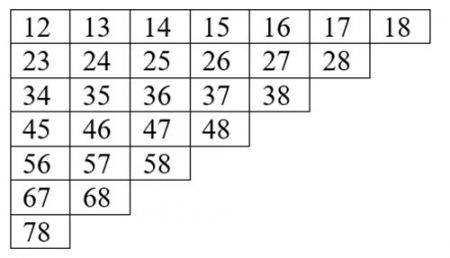
При встрече представителей большой восьмерки они обменялись рукопожатиями. Сколько всего было сделано рукопожатий?

Решение: Каждому представителю даем номер от 1 до 8, а рукопожатия закодируем следующим образом: например, число 24 означает что 2-ой представитель пожал руку 4-му. Причем число 35 и 53 означают одно и тоже рукопожатие, и брать будем меньшее из них. Коды рукопожатий мы можем оформить в виде таблицы.

Коды рукопожатий

Таким образом, у нас получилось 1+2+3+4+5+6+7=28 рукопожатий.

Пример 4

Бросаются две игральные кости. Сколько различных пар очков может появиться на верхних гранях костей?

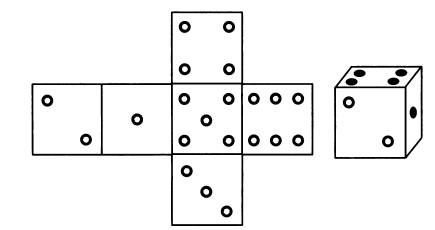
С помощью составленной ниже таблицы пар выпавших очков можно утверждать, что число всевозможных пар равно 6 · 6 = 36.

Следующий способ подсчета комбинаторных наборов является использование правила суммы: пусть объект a можно выбрать m способами, а объект b можно выбрать n способами, причём выбор одного объекта исключает одновременный выбор другого объекта. Тогда выбор "либо a, либо b" можно сделать m + n способами.

Пример 5

На подносе лежат 5 яблок и 3 груши. Сколькими способами можно выбрать фрукт с подноса?

Решение: Яблоко можно выбрать пятью способами. Грушу можно выбрать тремя способами. Стало быть, один из этих фруктов можно выбрать 5 + 3 = 8 способами.

Пример 6

Из класса нужно выделить одного дежурного, девочку или мальчика. Сколько существует способов для выбора дежурного, если в классе 20 мальчиков и 18 девочек?

Решение: выбрать одного мальчика из 20 мы можем 20-ю способами, а одну девочку из 18 можно 18-тью способами. Тогда выбрать одного дежурного мальчика или девочку можно (18+20) способами.

Бывают случаи, когда порядок, в котором идут выбранные элементы не важен, например, нужно из десяти человек выбрать троих дежурных. Такая операция называется неупорядоченной выборкой, или сочетанием. Всякая неупорядоченная выборка объёма k из множества, состоящего из n элементов, (k ≤ n) называется сочетанием из n элементов по k. Количество сочетаний обозначается C_n^k и вычисляется по формуле:

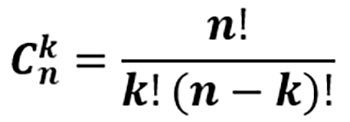
Пример 7

Преподаватель хочет назначить троих студентов для уборки аудитории. В группе двадцать семь студентов. Сколькими способами можно это сделать?

Решение: так как порядок студентов не важен, используем формулу для числа сочетаний (выбор любых 3 элементов из 27):

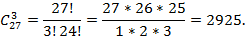
Упорядоченная выборка объёма k из множества, состоящего из n элементов, (k ≤ n) называется размещением из n элементов по k. Количество размещений обозначается A_n^k. Количество размещений из n элементов по k вычисляется по формуле:

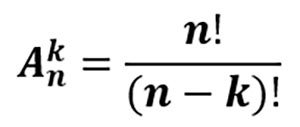
В частности, количество перестановок из n элементов по n элементов: A_n^k=P_n=n!

Пример 8

Расписание одного дня содержит 6 уроков. Определить количество таких расписаний при выборе из 12 дисциплин.

Решение: Выбор размещения определяется тем, что при построении расписания необходимо учитывать порядок следования уроков.

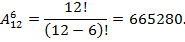
Пример 9

Сколькими способами семь конфет разных марок можно расставить на прилавке в один ряд?

Решение: эта задача о числе перестановок семи разных конфет. По формуле получаем: P7 = 7! = 1·2·3·4·5·6·7 = 5040 способов осуществить расстановку конфет.

В следующем примере применим правило произведения: пусть объект a можно выбрать m способами, после чего объект b можно выбрать n способами. Тогда упорядоченную пару (a, b) можно выбрать mn способами; иными словами, существует mn различных упорядоченных пар (a, b).

Пример 10

На библиотечной полке стоят 10 книг, причем 8 - книги разных авторов и еще 2 книги автора. Сколькими способами можно расставить эти книги так, чтобы книги одного автора стояли рядом друг с другом?

Решение: временно объединим три книги одного автора в один объект, всего получим 9 объектов - 8 книг и 1 объект из двух книг. Для них число перестановок будет P9. Теперь три книги переставим между собой P2 способами. По правилу произведения получаем что число способов расставить книги нужным образом равно: P9 · P2 = 9! · 2!

Этапы в обучении решению комбинаторных задач

Выделяют несколько этапов в обучении решению комбинаторных задач:

Первый этап – подготовительный. На данном этапе обучающиеся нарабатывают опыт образования каких-либо объектов из отдельных элементов.

На втором и третьем этапах процесс перебора происходит в определенной системе. На втором этапе решаются задачи с небольшим числом возможных вариантов, а на третьем – более сложные. Если обучение решению комбинаторных задач выходит за рамки урочной деятельности, то лучше всего воспроизвести игровую ситуацию, где дети сами будут выступать в роли элементов задачи.

Например: "Три-четыре ученика садятся на соответственное количество стульев в любом порядке. Затем они должны поменяться местами. Ставится вопрос: "Смогут ли дети каждый раз меняться местами так, чтобы их новое расположение оказывалось всё время отличным от предыдущих?" Варианты расположения детей фиксируются на доске. Данный процесс происходит до тех пор, пока не будут использованы все возможные варианты"

Чтобы облегчить процесс перебора вариантов, можно научить детей пользоваться такими средствами, как таблицы и графы. Решение комбинаторных задач с использованием таблиц и графов является основным содержанием третьего этапа.

Например: нарисуй и раскрась трехцветный флаг красным, белым и синим цветом с помощью таблицы.

Рассматривая таблицу, учащиеся "открывают" принцип ее составления, так как во время заполнения т нужно каждый раз определять, следует ли записывать данный вариант, не повторяется ли он.

Следующий метод, используемый при решении комбинаторных задач – графы. Граф-дерево используется для упорядочения вариантов при решении. Формирование умения решать задачи с помощью графов так же может происходить как во время уроков, так и во внеклассной или внеурочной работе.

Опять же обучение происходит поэтапно. На первом этапе решаются задачи с небольшим числом объектов. На втором постепенно идет увеличение количества объектов и связей между ними.

Например: Несколько приятелей при встрече пожали друг другу руки. Сколько встретилось приятелей, если рукопожатий было 10? В данной ситуации можно предложить ученикам рассмотреть последовательно варианты:

• если приятелей было двое (1 рукопожатие);
• если приятелей было трое (3);
• если приятелей было четверо (6);
• если приятелей было пятеро (10).

С увеличением количества объектов наступает необходимость введения основных правил комбинаторики. В основном это происходит в 7-9 классах, причем ученики должны понимать необходимость введения правил. В то же время вводятся понятия размещений, перестановок и сочетаний.