Метод Пирсона при решении текстовых задач по математике

В школьном курсе изучения математики, физики и химии часто встречаются задачи на смешивание различных веществ.

Для составления задач на растворы, смеси и сплавы приняты некоторые условия:

• все получающиеся смеси и сплавы однородны;
• для всех веществ выполняется закон сохранения массы (или объема): масса смеси нескольких веществ равна сумме масс компонентов.

Процентным содержанием (концентрацией или массовой долей) вещества в смеси называется отношение его массы к общей массе всей смеси. Это отношение может быть выражено либо в дробях, либо в процентах.

При решении задач методом Пирсона применяется схема:

Построим квадрат и начертим обе его диагонали. Слева от квадрата рядом с его вершинами запишем одну над другой процентное содержание растворенного вещества в исходных растворах, а в его центре – процентное содержание вещества в смеси, которую нужно приготовить, и общую массу вещества. Внутри квадрата у соответствующих вершин запишем массы взятых растворов.

Теперь выполним следующие действия:

1. Умножим выражения, стоящие внутри и снаружи квадрата, рядом с верхней, а затем и нижней вершинами. Согласно формуле, их сумма равна произведению чисел, стоящих в центре квадрата.
2. Вычтем от центра вдоль каждой диагонали квадрата процентные содержания веществ и запишем их, умножив на соответствующие массы исходных растворов.
   Получим выражения: (k – x1)∙m2 и (k – x2)∙m2. По формуле Пирсона сумма этих выражений равна 0.

Проанализировав задачи школьных учебников и сборников для подготовки учащихся к выпускным экзаменам, а так же банк заданий для подготовки к ГИА, были выделены 6 основных типов задач по построению условий.

Все остальные задачи являются либо комбинацией основных, либо требуют после решения уравнения дополнительных действий для нахождения искомой величины.

Решение 6 типов задач методом Пирсона

К 1 типу мы отнесли задачи с равным количеством веществ.

Пример: Смешали некоторое количество 15% раствора некоторого вещества с таким же количеством 19% раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?

Запись в схему Пирсона:

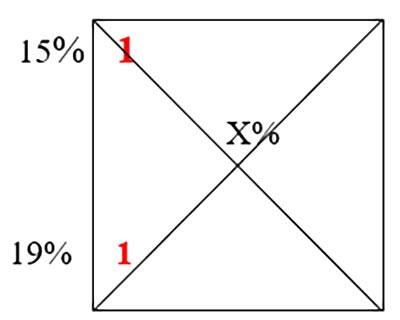
В этом случае массы запишем как единицы.
Составим уравнение:
(Х-15)*1+(Х-19)*1=0
Х=17 (кг)

2 тип - задачи с добавлением чистого вещества.

Пример: В сосуд, содержащий 5 литров 12% водного раствора некоторого вещества, добавили 7 литров чистой воды. Сколько процентов составляет концентрация получившегося раствора?
Запись в схему Пирсона:

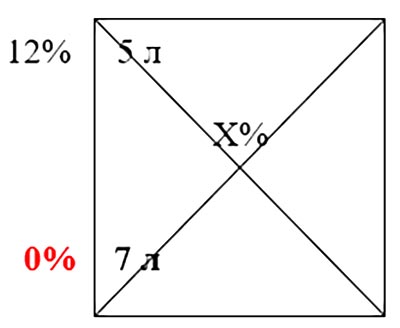
В этом случае концентрацию чистого вещества принимаем за 100% или 0%. Это зависит от вещества, концентрация которого учитывается в 1 веществе.
Составим уравнение:
(Х-12)*5+(Х-0)*7=0
Х=5%

3 тип - задачи, в которых известна масса полученной смеси.

Пример: Первый сплав содержит 5% меди, второй - 13% меди. Из этих двух сплавов получили третий сплав, массой 16 кг, содержащий 10% меди. Найдите массу первого сплава.

Запись в схему Пирсона:

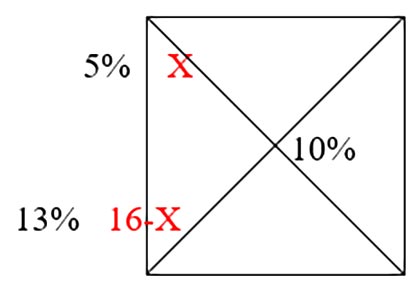
Масса смеси в уравнении не участвует, поэтому массу одного вещества обозначим Х, а другого – выразим как масса минус Х
Составим уравнение:
(10-5)*Х+(10-13)*(16-Х)=0
Х=6 (кг)

4 тип - задачи на сушку фруктов или грибов.

Пример: Свежие фрукты содержат 88% воды, а высушенные - 30%. Сколько требуется свежих фруктов для приготовления 6 кг высушенных фруктов?
Запись в схему Пирсона:

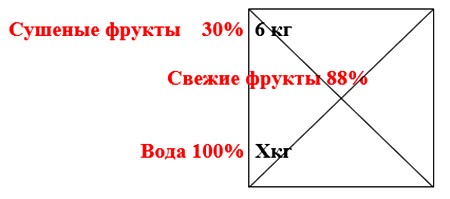
В этом случае сухие фрукты – примем за первое вещество, воду – за второе, а свежие фрукты – будем считать смесью.
Составим уравнение: (88-30)*6+(88-100)*Х=0
Х=29 (кг) воды; 6+29=35 (кг) свежих фруктов

5 тип - задачи на приготовление смеси из трех и более растворов.

Пример: Смешав 6 кг 30% и 5 кг 60% раствора кислоты и добавив чистой воды, получили 36% раствор кислоты. Сколько килограммов воды использовали для получения смеси?

Запись в схему Пирсона:

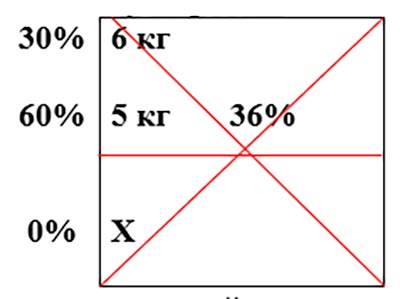
При записи условий внутри квадрата Пирсона рисуем не крест, а снежинку. И в уравнении будет три слагаемых.
Составим уравнение:
(36-30)*6+(36-60)*5+(36-0)*Х=0
Х=7/3 (кг)

6 тип - задачи на приготовление двух смесей из исходных растворов.

В этом случае строим 2 квадрата Пирсона, вводим две переменные и составляем систему из двух уравнений.

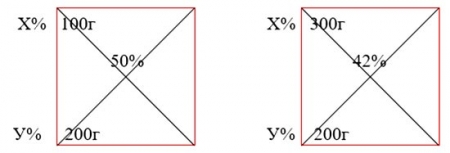
Пример: Имеется два раствора поваренной соли разной концентрации. Если слить вместе 100г первого раствора и 200 г второго, то получится 50% раствор. Если слить 300 г первого раствора и 200 г второго, то получится 42% раствор. Определить концентрации первого и второго растворов.

Схема Пирсона: задачи на приготовление двух смесей

Строим 2 квадрата Пирсона, вводим 2 переменные и составляем систему из двух уравнений:
(50-Х)*100+(50-У)*20=0, откуда Х=30%
(42-х)*300+(42-У)*200=0 У=60%

Решение комбинированных (сложных задач)

Задача 1.

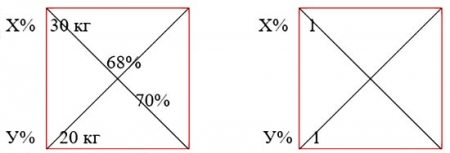
Имеется два сосуда. Первый содержит 30 кг, а второй - 20 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 68% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 70% кислоты. Сколько килограммов кислоты содержится в первом сосуде?

По 6 типу строим два квадрата Пирсона

По первому типу равные массы обозначаем за 1.
По 6 типу строим 2 квадрата Пирсона, вводим 2 переменные и составляем систему из двух уравнений.

(68-Х)*30+(68-У)*20=0, откуда Х=60%
(70-х)*1+(70-У)*1=0 У=80%

30*60%/100%=18 (кг)- масса чистой кислоты в 1 растворе.

Задача 2.

Имеется два сплава с разным содержанием золота. В первом сплаве содержится 35% золота, а во втором – 60%. В каком отношении надо взять первый и второй сплавы, чтобы получить из них новый сплав, содержащий 40% золота?

(40-35)*Х+(40-60)*У=0
5Х=20У
Х=4У

Сплавы надо взять в отношении 1:4.

Задача 3.

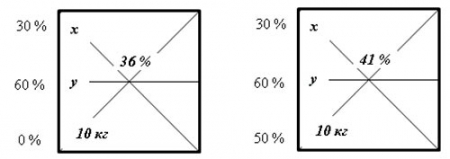
Смешав 30% и 60% растворы кислоты и добавив 10 кг чистой воды, получили 36% раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50% раствора той же кислоты, то получили бы 41% раствор кислоты. Сколько килограммов 30% раствора использовали для получения смеси?

По 2 типу концентрация чистой воды равна 0%.
По 5 типу для трех веществ строим вместо "креста" из диагоналей "снежинку" из трех лучей.
По 6 типу для двух смесей строим два квадрата, вводим две переменные и составляем систему из двух уравнений.

Пусть масса первого раствора равна х кг, а второго – y кг.
Заполним квадраты для трех растворов:

Решение сложных задач по методу Пирсона

Составим систему уравнений:

(41-30)*Х+(41-60)*У+(41-50)*10=0
(36-30)*Х+(36-60)*У+(36-0)*10=0

Из которой получаем Х = 54 (кг).