Учебный проект "Уникурсальные фигуры"

Проект "Уникурсальные фигуры" может быть использован во внеурочной деятельности для 5-6 классов.

Учебный проект «Уникурсальные фигуры" разработан учащимися 6 класса в рамках элективного курса «Измерение площади, объема». Содержание проекта выходит за уровень стандарта образования. Работа по проекту рассчитана две недели.

Цель проекта: создание сборника решений на уникурсальные фигуры.

Задачи проекта:

1. Исследовать понятие "уникурсальные фигуры".
2. Рассмотреть задачу о Кёнигсберских мостах.
3. Разработать инструкцию для решения уникурсальных фигур.
4. Привести собственное решение уникурсальных фигур.

Учебный проект поможет формированию таких умений, как умение самостоятельно работать, работать в команде, умение соотносить результат деятельности с целью и оценивать его, умение добывать информацию через Интернет, перерабатывать её, преобразовывать

 Задача о кёнигсбергских мостах

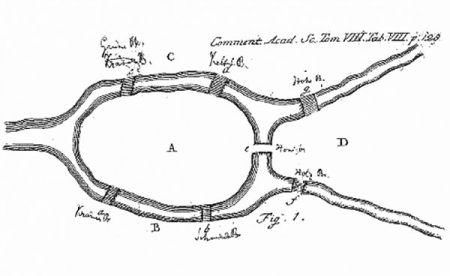
Однажды великому математику Леонарду Эйлеру был задан вопрос: можно ли обойти все семь мостов, стоявших тогда в городе Кёнигсберге (современный Калининград, Россия), побывав на каждом по одному разу?

Ниже приведена схема мостов.

Схема мостов Кёнигсберга

Рассмотрев эту задачу, в 1736 году Эйлер доказал, что это невозможно, причем он рассмотрел более общую задачу: какие местности, разделенные рукавами рек и соединенные мостами, возможно обойти, побывав на каждом мосту ровно один раз, а какие невозможно.

Эйлер придумал геометрическую модель к задаче.

Достаточно было построить еще один мост через Преголю, например соединяющий участки B и D, и задача обхода одним маршрутом восьми мостов, каждого по одному разу, становится разрешимой, сеть становится уникурсальной.

Вопрос положил начало новой увлекательной задаче: если дана геометрическая фигура, как начертить ее на бумаге одним росчерком пера, не проводя дважды ни одну линию? (уникурсальная фигура)

Скачать полную версию учебного проекта вы можете скачать по ссылке ниже