Олимпиадные задания по математике для 6 класса

Олимпиада по математике для учащихся 6 класса для проведения школьного этапа всероссийской олимпиады школьников в 2017-2018 учебном году.

В работе даны правильные варианты ответов и критерии оценивания работ.

Задание 1

Вася может получить число 100, используя десять троек, скобки и знаки арифметических действий:
100 = (33 : 3 - 3 : 3) · (33 : 3 - 3 : 3).
Улучшите его результат: используйте меньшее число троек и получите число 100.

Задание 2

Малыш, Алиса, Кай и Женя заняли первые четыре места в соревнованиях, причем никто из них не делил между собой какие-нибудь места. Известно:

Малыш не был ни первым, ни четвертым.
Алиса заняла второе место.
Кай не был последним.
Какое место занял каждый?

Задание 3

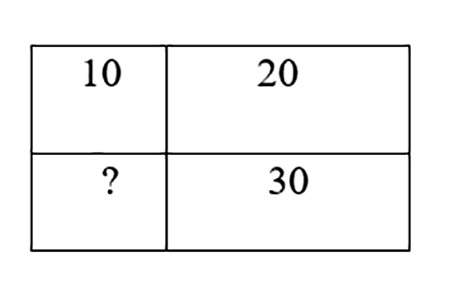
Прямоугольное поле ABCD состоит из четырех меньших прямоугольных полей (см. рисунок), три из которых имеют площади 10, 20, 30. Чему равна площадь поля ABCD?

Задание 4

Какова масса рыбы, если масса ее головы и туловища вместе 10 кг, туловища и хвоста – 8 кг, а головы и хвоста – 6 кг?

Задание 5

Отец старше сына в 4 раза, при этом суммарный их возраст составляет 50 лет. Через сколько лет отец станет старше сына в 3 раза?

Общие положения о проверке работ

Приведенные ниже решения задач не являются единственно возможными. Участники, вероятно, найдут и другие верные решения. При проверке и оценке решения учитывается только его верность и полнота. Приведенные ниже критерии по проверке задач также носят рекомендательный характер и могут быть уточнены и дополнены школьным жюри олимпиады в соответствии с особенностями решений школьников данной школы.

Каждая задача оценивается целым числом баллов от 0 до 7. Итог подводится по сумме баллов, набранных участником.

Основные принципы оценивания задач:

7 баллов - полное верное решение.

6-7 баллов - верное решение. Имеются небольшие недочеты, в целом не влияющие на решение

5-6 баллов - решение в целом верное. Однако оно содержит ряд ошибок, либо не рассмотрение отдельных случаев, но может стать правильным после небольших исправлений или дополнений.

4 балла - верно рассмотрен один из двух (более сложный) существенных случаев.

2-3 балла - доказаны вспомогательные утверждения, помогающие в решении задачи.

1 балл - рассмотрены отдельные важные случаи при отсутствии решения (или при ошибочном решении).

0 баллов - решение неверное, продвижения отсутствуют.

0 баллов - решение отсутствует.

Олимпиадная работа не является контрольной работой участника, поэтому любые исправления в работе, в том числе зачеркивание ранее написанного текста, не являются основанием для снятия баллов.

Недопустимо снятие баллов в работе за неаккуратность записи решений при ее выполнении. Баллы не выставляются "за старание участника", в том числе за запись в работе большого по объему текста, но не содержащего продвижений в решении задачи. Победителем в параллели считается участник, набравший наибольший суммарный балл и решивший не менее половины задач (не менее трех задач).

Победителей в параллели может быть несколько. Призерами рекомендуется считать участников, решивших не менее половины задач, но набравших меньше баллов, чем победитель. Если ни один участник в данной параллели не решил более двух задач, жюри может принять решение считать призерами участников, решивших две задачи, однако победителей в этом случае не будет.

Ответы на задания олимпиады по математике

Решение задания 1
Один из вариантов, не самый короткий, предусматривает использование 8 троек:
(33 - 3) : 3 · (33 - 3) : 3 = 100
Аналогично: (333 - 33) : 3 = 100.

Ответ на задание 2
Малыш - 3, Алиса - 2, Кай - 1, Женя - 4 место.

Ответ на задание 3
? = 15, а общая площадь равна 75.

Решение задания 4
Масса рыбы 12 кг.
Г + Т = 10, Т + Х = 8, Г + Х = 6, 2( Г + Т + Х)= 24, Г + Т + Х =12.

Решение задания 5
Пусть сыну сейчас x лет, отцу - 4x лет, тогда x+4x=50.
Сыну сейчас 10 лет, а через y лет будет 10+y лет, а отцу 40+y лет 3(10+y) = 40+y; y=5
Ответ: через 5 лет.