Олимпиадные задания по математике для 5 класса

Главная » Средние классы » Тесты и олимпиады

Олимпиада по математике состоит из 5 задач с ответами и критериями оценивания.

Общее максимальное количество баллов - 35 (по 7 б. за каждое задание).

Задания олимпиады по математике

Задание № 1
Можно ли число 1000 выразить восемью одинаковыми цифрами? При этом, кроме цифр, разрешается пользоваться также знаками действий.

Задание № 2
В королевстве 1001 город. Король приказал проложить между городами дороги так, чтобы из каждого города выходило ровно 7 дорог. Смогут ли подданные справиться с приказом короля?

Задание № 3
Из девяти монет одна фальшивая: она легче остальных. Как за два взвешивания на чашечных весах без гирь определить, какая именно фальшивая?

Задание № 4
Ковер-самолет имеет форму прямоугольника со сторонами 10 м и 11 м. Докажите, что Старик Хоттабыч и Волька сумеют разрезать его на шесть квадратных ковриков.

Задание № 5
В летний лагерь приехали отдыхать три друга: Миша, Володя и Петя. Известно, что каждый из них имеет одну из следующих фамилий: Иванов, Семенов, Герасимов. Миша — не Герасимов. Отец Володи — инженер. Володя учится в 6 классе. Герасимов учится в 5 классе. Отец Иванова — учитель. Какая фамилия у каждого из трех друзей?

Критерии оценивания заданий

Решение:
1 решение 888+88+8+8+8=1000
2 решение (2222 – 222) / 2 = 1000
Во втором решении цифру 2 можно заменить на любую другую (разумеется, кроме нуля).

Ответ: можно.

Баллы	Критерии оценивания задания № 1
7	Полное верное решение или приведены два и более способа решения
6	Приведен один пример
4	Решение в целом верное. Однако оно содержит ошибки, но может стать правильным после небольших исправлений или дополнений
0	Решение неверное, продвижения отсутствуют ИЛИ решение отсутствует, записан только номер задания

Решение: 1001х7=7007 – всего должно выходить дорог, но мы посчитали каждую дорогу дважды. Значит, на самом деле должно быть проложено 7007:2=3503,5 дорог, чего сделать не получится.

Ответ: не смогут.

Баллы	Критерии оценивания задания № 2
7	Полное верное решение.
6	Решение верное. Имеются недочеты, в целом не влияющие на решение. Имеются небольшие недочеты, в целом не влияющие на решение. ИЛИ верное решение, но не записан ответ.
5	Решение и идея решения задания в целом верные. Однако в одном из действий допущена ошибка. Решение может стать правильным после небольших исправлений или дополнений
3	Приведены верные рассуждения, но допущена логическая ошибка. Решение может стать правильным после исправлений или дополнений
2	Найдена идея решения, но оно не доведено до конца.
1	Верно указан ответ при отсутствии решения
0	Решение неверное, продвижения отсутствуют ИЛИ решение отсутствует, записан только номер задания.

Задание № 3
Из девяти монет одна фальшивая: она легче остальных. Как за два взвешивания на чашечных весах без гирь определить, какая именно?

Решение:

Разобьем монеты на 3 кучки по 3 монеты и проведем взвешивания.
1 взвешивание: положим по 3 монеты на каждую чашку весов.
Возможны два случая:
1. Равновесие, значит, на весах только настоящие монеты, а фальшивая среди тех монет, которые не взвешивались.
2. Одна из кучек легче, в ней фальшивая монета.
2 взвешивание: теперь требуется найти фальшивую среди трех монет (по методу первого взвешивания).

Баллы	Критерии оценивания задания № 3
7	Полное верное решение
6	Верное решение. Имеются небольшие недочеты, в целом не влияющие на решение. Полное верное решение, но не записан ответ
5	Решение в целом верное. Однако оно содержит ошибки, но может стать правильным после небольших исправлений или дополнений
4	Решение в целом верное. Однако оно содержит пропуск отдельных случаев, но может стать правильным после исправлений или дополнений
3	Задача решена «наполовину», ход решения правильный, есть прогресс в решении, но полное решение требует дополнительных существенных идей
2	Найдена идея решения, но оно не доведено до конца
1	Записан верный ответ при отсутствии решения (или при ошибочном решении)
0	Решение неверное, продвижения отсутствуют. ИЛИ Решение отсутствует, записан только номер задания

Задание № 4
Ковер-самолет имеет форму прямоугольника со сторонами 10 м и 11 м. Докажите, что Старик Хоттабыч и Волька сумеют разрезать его на шесть квадратных ковриков.
Решение:

1 способ (словесный)
Квадраты могут быть разного размера.
Пусть по горизонтали 11 м, а по вертикали 10 м.

Вертикально отрежем слева полосу 5х10, которую разрезаем на два квадрата 5х5.
Остался прямоугольник 6х10. Снизу от оставшегося куска отрезаем квадрат 6х6.
Остается кусок 4х6. Справа от этого куска отрезаем квадрат 4х4.
Остается полоска 2х4, которая режется на 2 квадрата 2х2.

Получили6 квадратов: 6х6 м - 1 штука, 5х5 м - 2 штуки, 4х4 м - 1 штука, 2х2 м - 2 штуки.
Проверяем: 6*6 + 2*5*5 + 4*4 + 2*2*2 = 36 + 50 +16 + 8 = 110 = 10*11.

2 способ (наглядный, с указанием размеров).

Наглядный способ решения

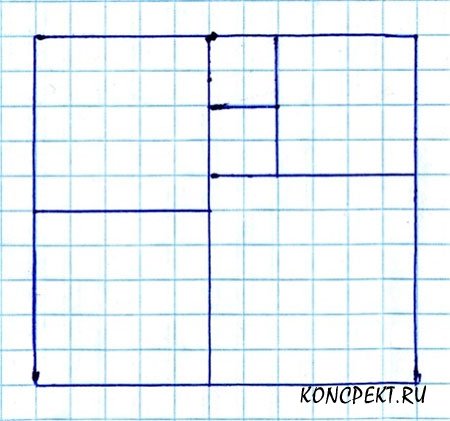
Баллы	Критерии оценивания задания № 4
7	Полное верное решение. Приведено словесное описание или наглядное
6	Верное решение. Имеются небольшие недочеты, в целом не влияющие на решение
5	Решение в целом верное. Однако оно содержит ряд ошибок, но может стать правильным после небольших исправлений или дополнений
4	Решение и идея решения задания в целом верные. Однако в одном из действий допущена ошибка. Например, указан неверный способ разрезания фигуры. Решение может стать правильным после небольших исправлений или дополнений.
3	Рассуждения в целом верное. Однако оно содержит ряд ошибок, либо пропуск отдельных случаев, но может стать правильным после небольших исправлений или дополнений.
2	Найдена идея решения, но оно не доведено до конца
1	Записан (показан) размер только одного квадрата.
0	Решение неверное, продвижения отсутствуют ИЛИ Решение отсутствует, записан только номер задания

Решение:

Так как Володя учится в 6 классе, а Герасимов в 5 классе, то Володя — не Герасимов. Так как отец Иванова — учитель, отец Володи — инженер, то Володя — не Иванов. Тогда Володя — Семенов, Миша — Иванов, а Петя — Герасимов.
Можно для наглядности применить графы или таблицы.

Ответ: Миша – Иванов, Володя – Семенов, Петя – Герасимов.

Баллы	Критерии оценивания задания № 5
7	Ход решения верный, все шаги его выполнены, получен верный ответ
6	Ход решения верный, все шаги его выполнены. Имеются недочеты (даны неполные объяснения), в целом не влияющие на решение. ИЛИ полное верное решение, но не записан ответ
5	Решение содержит незначительные ошибки в рассуждениях, пробелы в обоснованиях, но в целом верно и может стать полностью правильным после небольших исправлений или дополнений
4	Решение в целом верное и полное. Однако оно содержит ряд ошибок, либо пропуск отдельных случаев, но может стать правильным после небольших исправлений или дополнений
3	Решение начато правильно, не доведено до конца
2	Записан верный ответ при отсутствии рассуждения (или при ошибочном рассуждении)
0	Задание не решено (неверное решение)