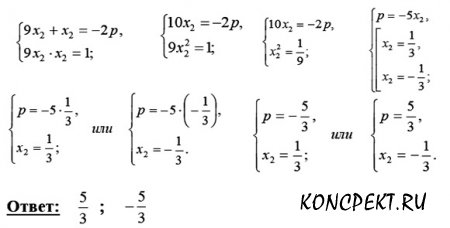Олимпиада по математике для учащихся 8 класса

Олимпиада по математике для 8 класса состоит из 5 заданий. Общее время выполнения работы – 4 урока, 180 минут.

Общее максимальное количество баллов - 35 (по 7 баллов за каждое правильно выолненное задание).

Задание № 1
45 конфет стоят столько же рублей, сколько их можно купить на 20 рублей. Сколько конфет можно купить на 50 рублей?

Задание № 2
При каких значениях параметра р отношение корней уравнения x2 + 2px +1 = 0 равно 9?

Задание № 3
Мальчик стоит на автобусной остановке, а автобуса нет. Ему хочется пройтись до следующей остановки. Мальчик бегает вчетверо медленнее автобуса и может увидеть автобус на расстоянии 2 км. До следующей остановки ровно километр. Имеет ли смысл идти, или есть риск упустить автобус?

Задание № 4
В трапеции длина одной из диагоналей равна сумме длин оснований, а угол между диагоналями равен 60°. Докажите, что трапеция – равнобедренная.

Задание № 5
Докажите, что в любой компании найдутся два человека, имеющие равное число знакомых в этой компании (если A знаком с B, то и B знаком с A).

 

Ответы и критерии оценивания олимпиады по математике

Решение задания № 1

Пусть x — стоимость одной конфеты в рублях. Тогда 45x = 20/x , откуда x = 2/3 . Тогда на 50 рублей можно купить 50/x = 75 конфет.
Ответ: 75 конфет.

Баллы

Критерии оценивания задания №1

7

Приведено полное обоснованное решение и получен верный ответ.

6

Верно и обосновано получено необходимое равенство, но допущена вычислительная ошибка, не повлиявшая на ответ.

5

Необходимое равенство получено, но дальнейших продвижений нет.

4

Приведено частное решение задачи с конкретными числами и сделан правильный вывод.

1

Приведен только ответ.

0

Приведено неверное решение или оно отсутствует.

Решение задания № 2

Пусть x1 = 9x2, тогда по теореме Виета:

Ответ к заданию № 2 олимпиады по математикеОтвет к заданию № 2 олимпиады по математике

Баллы

Критерии оценивания задания № 2

7

Полное верное обоснованное  решение.

6

Верное решение. Имеются небольшие недочеты, в целом не влияющие на решение. Или  полное верное решение, но не записан ответ.

5

Верное рассуждение, но решение не доведено до конца и найден только один корень.

2

Правильно найден дискриминант. Дальнейшие продвижения  в решении задачи отсутствуют.

0

Решение неверное, продвижения отсутствуют или решение отсутствует, записан только номер задания.

Решение задания № 3

Пусть мальчик пробежит х км, тогда автобус проедет 4х км. Если они двигаются навстречу друг другу, до встречи с автобусом мальчик пробежит 2/5 км (из уравнения 4х+х=2). Это значит, что, отойдя от остановки не более, чем на 2/5 км, мальчик сможет успеть на автобус, побежав назад.

Если автобус догоняет мальчика, мальчик успеет пробежать 2/3 км до момента, когда автобус его догонит (из уравнения 4х-х=2). Это означает, что он сможет успеть на автобус, если до следующей остановки осталось не более 2/3 км, то есть, если он успел пройти не менее 1/3 км до момента, когда заметил автобус. Так как, 1/3 < 2/5 , то у мальчика всегда будет возможность успеть на автобус и имеет смысл идти.

Ответ: да, имеет смысл идти.

Баллы

Критерии оценивания задания № 3

7

Полное верное решение.

6

Решение верное. Имеются недочеты, в целом не влияющие на решение.

5

Верное решение, но не записан ответ.

4

Решение содержит пробелы в обоснованиях, но в целом верно и может стать полностью правильным после небольших исправлений или дополнений. Записан правильный ответ.

3

Рассмотрены отдельные шаги решения и сделан правильный вывод.

2

Решение не доведено до конца и получен неверный  ответ.

1

Записан ответ без объяснения.

0

Задание не решено (неверное решение).

Решение задания № 4

Рисунок к олимпиадному заданию по математике № 4

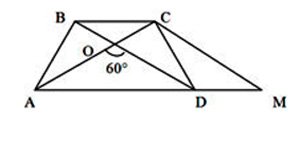
Пусть AD = a, BC = b, AC = a + b. Продолжим AD за точку D на расстояние DM = BC. ΔАСМ - равносторонний. Но это значит, что ΔАОD и ΔВОС - тоже равносторонние.

Отсюда следует, что ∠ АОВ = ∠ СОD, откуда имеем, что AB = CD.

Баллы

Критерии оценивания задания № 4

7

Верное обоснованное решение задачи.

6

Приведены верные рассуждения, являющиеся решением задачи, но по каким-либо причинам дан неверный ответ (например, указан угол СDО вместо угла СОD).

5

Приведены в целом верные рассуждения, в которых допущены ошибки, не имеющие для сути решения принципиального характера, и дан верный ответ.

4

Приведено схематичное решение задачи при отсутствии обоснований: указаны все промежуточные выводы без указания связей между ними (ссылок на теоремы или определения).

1

Сделаны дополнительные построения и обозначения на чертеже, из которых ясен ход решения, дан верный ответ, но не приведены сами рассуждения.

0

Задание  не решено (неверное решение) или записан ответ без объяснения.

Решение задания № 5

Пусть в компании k человек. Тогда каждый человек может иметь от нуля до (k – 1) знакомых. Предположим противное: количество знакомых у всех разное. Тогда найдется человек без знакомых, найдется человек с одним знакомым, и так далее, наконец, найдется человек, у которого (k – 1) знакомых.

Но тогда этот последний знаком со всеми, в том числе и с первым. Но тогда у первого не может быть ноль знакомых. Получили противоречие.

Баллы

Критерии оценивания задания № 5

7

Ход решения верный, все шаги его выполнены, утверждение доказано.

6

Ход решения верный, все шаги его выполнены. Имеются недочеты (даны неполные объяснения), в целом не влияющие на решение.

4

Верно выполнены рассуждения, но допущена логическая ошибка. Решение может стать правильным после небольших исправлений или дополнений.

2

Рассмотрены отдельные шаги решения. Указаны вариант раскрашивания доски в два цвета и количество закрашенных клеток.  Или решение не доведено до конца.

0

Задание не решено (неверное решение).
olimpiada.rar
Размер:
30.34 Kb
Скачали:
34

Метки к статье: Олимпиада, математика, 8 класс

конспект.ru рекомендует: