Конспект урока геометрии 8 класс "Теорема Пифагора и ее применение при решении задач"

Главная » Средние классы » Конспекты уроков » Математика 8 класс

Цель урока:

закрепить знание определения и следствий теоремы Пифагора;
научиться решать задачи по данной теме;
осуществление межпредметной связи геометрии с алгеброй, историей, повседневной жизнью.

Ход урока

Организационный этап

Учитель: Ребята, здравствуйте!
Я попрошу сейчас вас всех обернуться и взглядом найти какую-нибудь дальнюю точку. И зафиксируйте на ней свой взгляд. Обернитесь еще раз и попробуйте отвести взгляд еще дальше. Получилось? Замечательно!

Присаживайтесь. Человек всегда может расширять свои возможности. У вас сначала было одна точка а вы смогли добиться еще большего и лучшего результата.
И я хочу ч тобы вы сегодня расширили свои знания по той теме, которую мы с вами сегодня будем изучать

Рада всех уроке. Хочу пожелать всем интересного и плодотворного занятия. Давайте начнем!
Мы продолжаем изучение одной из самых известных теорем древности, теорему Пифагора. Значение теоремы Пифагора состоит и в том, что с ее помощью можно доказать многие другие теоремы и решить множество задач.

Как вы думаете что сегодня мы будем делать на уроке? (ответы учащихся)
Открываем тетради и записываем тему урока.
Какие цели мы сформулируем сегодня на урок?

Проверка домашнего задания

Учитель: Мы продолжаем знакомиться с одной из самых древних и важных наук - геометрией. Давайте вспомним, какой теореме вы говорили с вами на прошлом уроке. О жизни Пифагора.

На предыдущем уроке мы с вами рассмотрели теорему Пифагора - одну из главных и можно сказать самых главных теорем геометрии. Значение ее состоит в том, что из нее или с ее помощью можно вывести большинство теорем геометрии.

У этой теоремы есть не только различные названия и доказательства, но и формулировки самой теоремы с течением времени менялись. Вы дома должны были найти эти формулировки.

У Евклида эта теорема гласит (дословный перевод): "В прямоугольном треугольнике квадрат стороны, натянутой над прямым углом, равен квадратам на сторонах, заключающих прямой угол".

Во времена Пифагора теорема была сформулирована так: «Доказать, что квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на катетах»

Латинский перевод арабского текста Аннаирици (около 900 г. до н. э.), сделанный Герхардом Кремонским (начало 12 в.), в переводе на русский гласит: "Во всяком прямоугольном треугольнике квадрат, образованный на стороне, натянутой над прямым углом, равен сумме двух квадратов, образованных на двух сторонах, заключающих прямой угол".

В Geometria Culmonensis (около 1400 г.) теорема читается так:

Also, wird das vierecke Feld, gemessen an der langen Wand, so also gross ist als bei beide Vierecke, bei zwei werden gemessen von den zwei Wanden des deren, bei zwei gemeinde, tretten in dem rechten Winkel.

В переводе это означает: "Итак, площадь квадрата, измеренного по длинной стороне, столь же велика, как у двух квадратов, которые измерены по двум сторонам его, примыкающим к прямому углу"

Современная формулировка теоремы Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов

А вот формулировка теоремы Пифагора в стихотворном виде:

Если дан нам треугольник,
И притом с прямым углом,
То квадрат гипотенузы
Мы всегда легко найдем:

Катеты в квадрат возводим,
Сумму степеней находим -
И таким простым путем,
К результату мы придем.

Вы нашли 6-8 различных формулировок, а вот доказательств этой теоремы на данный момент в научной литературе зафиксировано 367. Очевидно, теорема Пифагора является единственной теоремой со столь внушительным числом доказательств.

И поэтому она внесена в книгу рекордов Гиннеса. Такое многообразие можно объяснить лишь фундаментальным значением теоремы для геометрии.

Актуализация опорных знаний

Эпиграфом сегодняшнего нашего урока будут слова немецкого астронома и математика Иоганна Кеплера который еще в XVII веке сказал, что геометрия обладает двумя великими сокровищами. Первое – это теорема Пифагора, которую можно сравнить с мерой золота…

Для того, чтобы наша работа была успешной, давайте повторим некоторые геометрические факты.

Какой треугольник называется прямоугольным?

Как называются стороны прямоугольного треугольника?

Как звучит теорема Пифагора?

Один из углов прямоугольного треугольника равен 15°. Чему равны остальные углы?

Один из углов из углов прямоугольного треугольника равен 30°, катет, противолежащий ему, равен 13 см. Чему равна гипотенуза?

Катет прямоугольного треугольника равен 16 дм, гипотенуза – 32 дм. Найдите углы треугольника.

Пифагор - это не имя, а прозвище, которое философ получил за то, что всегда говорил верно и убедительно, как греческий оракул. (Пифагор - "убеждающий речью")

Выполним несколько устных упражнений, которые пригодятся на уроке:
Вычислите:
11²; 25²; 4²; 20²; 12²
√400; √169 ; √225; √8; √4225 ; √(-16)
Х² = 144; Х² = 11

Тест "Вспомни"

Вот сейчас с помощью теста мы и проверим, насколько уверенно вы ориентируетесь в теореме Пифагора. На парте желтые листочки! Тест несложный, но их результаты будут учтены при выставлении оценки за урок. У вас 1 минута. (обвести кружочком правильный ответ)

К каким треугольникам можно применить теорему Пифагора?
а) любым;
б) прямоугольным;
в) равносторонним

2. Верно ли, что в прямоугольном треугольнике любой из катетов меньше гипотенузы?
а) нет;
б) не знаю;
в) да

3. Гипотенуза прямоугольного треугольника равна 5 см, катет 3 см. Найти длину второго катета?
а) 8 см;
б) 4 см;
в) 10 см

4. Теорема Пифагора записывается так:
а) а² = с² - в²
б) в² = с² – а²
в) с² = а² + в²

5. В прямоугольном треугольнике углы могут быть равны:
а) 90; 60; 90;
б) 45; 90;45;
в) 60; 30; 60

Закрепление материала

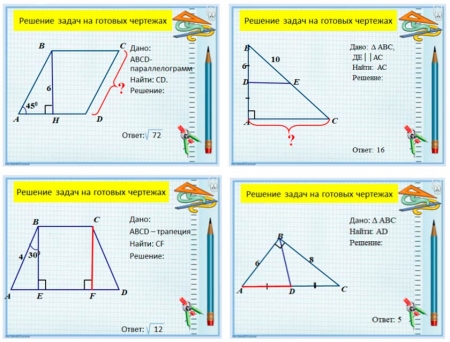
Решение задач на готовых чертежах у доски.

Задачи по теореме Пифагора

Физминутка

Рисуй глазами треугольник.
Теперь его переверни
Вершиной вниз.
И вновь глазами

Ты по периметру веди.
Рисуй восьмерку вертикально.
Ты головою не крути,
А лишь глазами осторожно

Ты вдоль по линиям води.
И на бочок ее клади.
Теперь следи горизонтально,
И в центре ты остановись.

Зажмурься крепко, не ленись.
Глаза открываем мы, наконец.
Зарядка окончилась.
Ты – молодец!

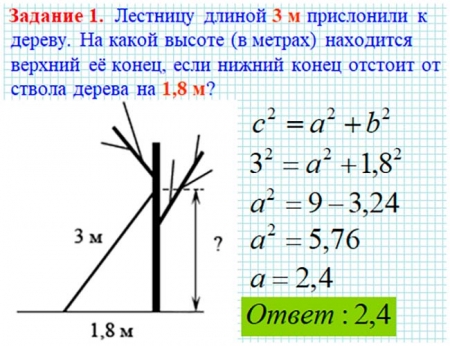
Задача из банка ОГЭ
Лестницу длиной 3 м прислонили к дереву. На какой высоте (в метрах) находится верхний ее конец, если нижний конец отстоит от ствола дерева на 1,8 м?

Рисунок к задаче

Задача из банка Региональный экзамен по геометрии
Два теплохода вышли из порта, следуя один на север, другой на запад. Скорости их равны соответственно 10 км/ч и 24 км/ч. Какое расстояние (в километрах) будет между ними через 2 часа?

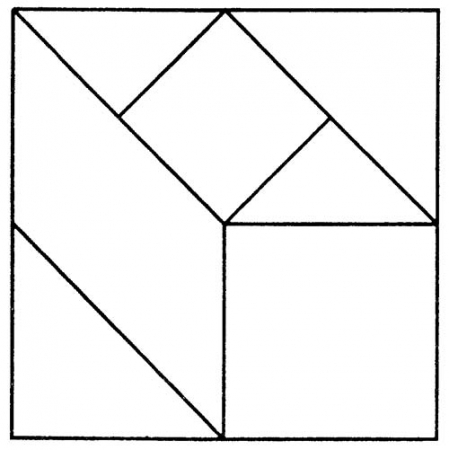
Пифагорейская головоломка

Из семи частей квадрата составить снова квадрат, прямоугольник, равнобедренный треугольник, трапецию.

Пифагорейская головоломка

Составьте из нескольких фигур (задание по группам)

1 группа: треугольник. (к маленькому квадрату по очереди присоеденить 2 маленьких треугольника)
2 группа: прямоугольник.
3 группа: трапеция.

Возьмите большой и маленький треугольник и составьте четырехугольник, чтобы получился прямоугольник. Что нужно добавить? (маленький треугольник)
Берем четырехугольник, 2 маленьких треугольника и маленький квадрат. Составьте прямоугольник.
Молодцы! А теперь с помощью всех геометрических фигур составьте квадрат.

Итог урока

Какую цель поставили вначале урока?
Достигли мы цели?

Каким образом, мы достигли цель?
Удалось ли вам расширить свои знания и возможности при изучении данной темы?

Домашнее задание

Подготовить презентацию по теме: Применение теоремы Пифагора.

Рефлексия

У каждого на столе лежат карточки. Необходимо из предложенных вариантов выбрать, отметить и озвучить 5 предложений, близких каждому по ощущениям, по теме урока.
Выбери 5 любых предложений: