Решение задач по теме "Дроби"

В соответствии с требованиями к результатам освоения программы по математике в 5-6 классах обучающиеся должны научиться решать задачи на нахождение части числа и числа по его части.

Кроме того, должны получить возможность научиться решать и обосновывать свое решение задач на нахождение части от числа и числа по его части на основе конкретного смысла дроби. Рассмотрим способы решения этих задач.

Пример задачи на нахождение части от числа

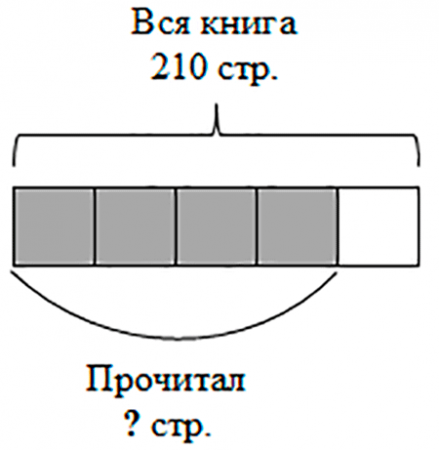
Елисей прочитал 4/5 книги, в которой 210 страниц. Сколько страниц прочитал Елисей?

Вся книга – 210 страниц. Дробь 4/5 показывает, что Елисей прочитал четыре части книги из пяти.

Рисунок к задаче на нахождение части от числа

1) 210 : 5 = 42 (стр.) – это одна пятая часть книги.
2) 42 ∙ 4 = 168 (стр.)

Ответ: Елисей прочитал 168 страниц.

Замечание 1. Если ребенок понимает смысл дроби (знаменатель показывает, на сколько частей разделили целое, а числитель – сколько из этих частей взяли), то изображение дроби в виде рисунка не вызывает затруднений. Далее по условию задачи нужно определить, что известно: целое или часть. Указать это на краткой записи.

Замечание 2. Некоторые дети путают числитель и знаменатель. В этом случае поможет такая аналогия: Человек/Земля (Человек стоит на Земле. Числитель над Знаменателем).

Пример задачи на нахождение числа по его части

В саду росло 28 яблонь, что составляло 7/8 всех деревьев сада. Сколько всего деревьев росло в саду?

Дробь 7/8 показывает, что яблони составляют семь частей из восьми.

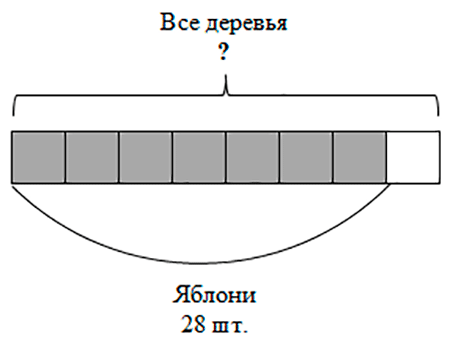
1) 28 : 7 = 4 (д.) – это одна седьмая часть всех деревьев сада.
2) 4 ∙ 8 = 32 (д.)

Ответ: в саду росло 32 дерева.

Замечание. Главное – правильно составить краткую запись. Определить, что 28 – это не все деревья в саду, а их часть. Тогда по рисунку видно, что число 28 изображено в виде семи частей. Чтобы найти одну часть, нужно 28 разделить на 7.

Примеры более сложных задач по теме "Дроби"

Пример 1

Купили 14 кг сахара. На варенье израсходовали 5/7 сахара. Сколько килограммов сахара осталось?

I способ

Дробь 5/7 показывает, что израсходовали пять частей сахара из семи.

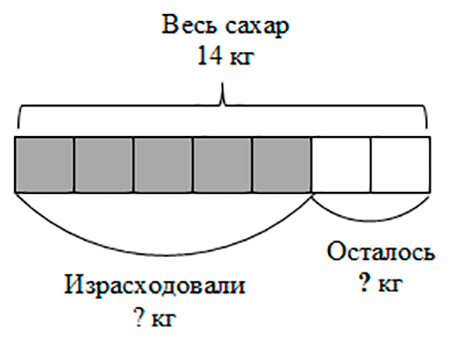
1) 14 : 7 = 2 (кг) – это одна седьмая часть всего сахара.
2) 2 ∙ 5 = 10 (кг) – сахара израсходовали.
3) 14 – 10 = 4 (кг)

Ответ: осталось 4 кг сахара.

II способ

Дробь 5/7 показывает, что израходовали пять частей сахара из семи.

1) 14 : 7 = 2 (кг) это одна седьмая часть всего сахара.
2) 7 – 5 = 2 (части) сахара осталось.
3) 2 ∙ 2 = 4 (кг)

Ответ: осталось 4 кг сахара.

Пример 2

Число увеличили на четверть от самого числа, и получилось 625. Найдите исходное число.
Замечание. Подобного типа задания встречаются на всероссийских проверочных работах по математике в 6 классе. Источники в интернете предлагают решение таких задач с помощью уравнений, используя алгебраический способ.

Проблема в том, что при данном способе решения нужно не только правильно составить уравнение, но и решить его без ошибок. Можно предложить альтернативный вариант решения задания, используя только смысл дроби.

Алгебраический способ решения

Обозначим исходное число х. Тогда четверть от этого числа – это 1/4 x. Так как число увеличили на четверть от самого числа, и получилось 625, то составляем уравнение:

x + 1/4x = 625
5/4x = 625
x = 625 ∙ 4/5
x = 500

Ответ: 500.

Способ решения, основанный на понимании смысла дроби

Так как число увеличили на четверть от самого числа, то исходное число делится на 4. Изобразим его в виде четырех частей и дорисуем еще одну часть (добавим четверть). Все вместе – 625.

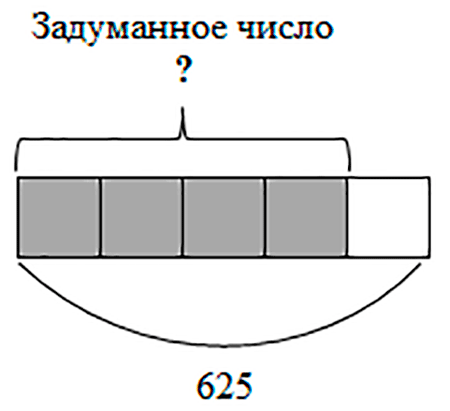
По рисунку видно, что число 625 составляет пять частей. А задуманное число – четыре части.

625 : 5 ∙ 4 = 500
Ответ: 500

Пример 3

Если задуманное число умножить на три, то результат окажется на 210 больше половины задуманного числа. Найдите задуманное число.

Алгебраический способ решения

Обозначим задуманное число х. Задуманное число умножили на 3, получили 3x. Результат на 210 больше половины задуманного числа. Получим уравнение:

3x = 1/2x + 210.
3x - 1/2x = 210.
5/2x = 210.
x = 210 ∙ 2/5.
x = 84.

Ответ: 84.

Способ решения, основанный на понимании смысла дроби

Изобразим задуманное число одной клеткой. Увеличим его в три раза (равносильно умножению на три). Отметим половину задуманного числа.

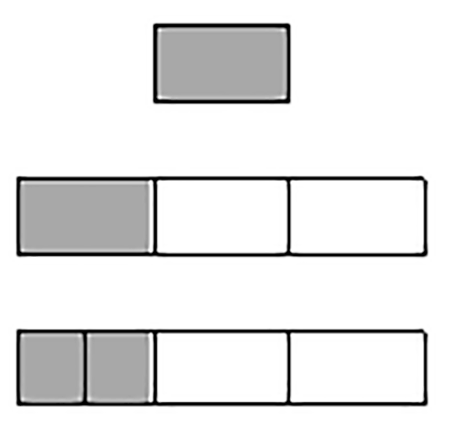
Отметим, что результат (то есть три большие клетки) больше на 210, чем половина задуманного числа.

По рисунку заметим, что число 210 изображено с помощью неравных частей. Разобьем две большие части на половинки.

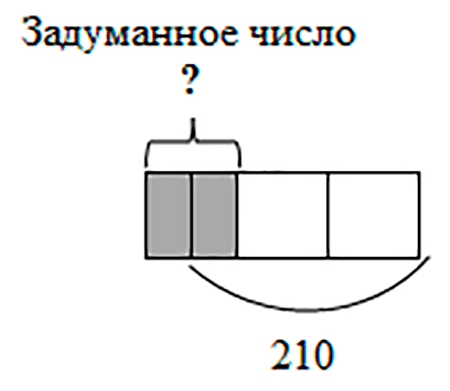
Теперь, глядя на рисунок, заметим, что число 210 – составляет пять равных частей, а задуманное число – две части.

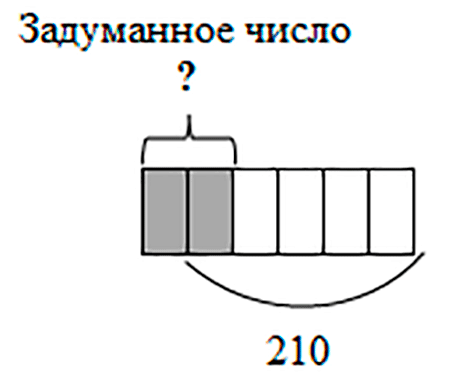
210 : 5 ∙ 2 = 84.

Ответ: 84.

Замечание. Способ решения каждый выбирает для себя. Если ученики умеют изображать дроби схематически, видеть и выделять нужные части, то второй способ не вызывает затруднений и экономит время на решение.