Практическая работа по алгебре на тему "Построение графиков функций"

Раздел: Функции, их свойства и графики.

Учебная цель:

• расширить представление о приемах построения графиков, актуализация знаний и умений;
• обобщить все имеющиеся знания об элементарных функциях, их графиках, способах задания, функции, области определения и области значений.

Учебные задачи:

• довести до сведения обучающихся возможные преобразования графиков функций с помощью параллельного переноса и растяжения вдоль координатных осей;
• отработка алгоритма построения графиков с помощью геометрических преобразований;
• формирование практических умений и навыков построения и чтения графиков функций;
• иметь наглядные представления об основных свойствах функциях, "читать" свойства функций по графику;
• находить по графику промежутки возрастания и убывания, промежутки знакопостоянства, наибольшее и наименьшее значения; иллюстрировать их с помощью графических изображений;
• уметь строить графики функций;
• применять правила преобразований: параллельного переноса, сжатия и растяжения, отражения графиков относительно осей.

Образовательные результаты, заявленные в ФГОС:

Студент должен

уметь:

• построить график не только элементарных функций, но и более сложных;
• применять геометрические преобразования при построении графиков функций

знать:

• понятие числовой функции;
• область определения функции;
• область значения функции;
• аргумент функции;
• график функции;
• геометрические преобразования.

Краткие теоретические и учебно-методические материалы по теме практической работы

В чистом виде основные элементарные функции встречаются, к сожалению, не так часто. Гораздо чаще приходится иметь дело с элементарными функциями, полученными из основных элементарных при помощи добавления констант и коэффициентов. Графики таких функций можно строить, применяя геометрические преобразования к графикам соответствующих основных элементарных функций (или переходить к новой системе координат).

К примеру, квадратичная функция:

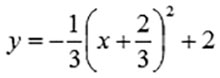
представляет собой квадратичную параболу y = x2, сжатую втрое относительно оси ординат, симметрично отображенную относительно оси абсцисс, сдвинутую против направления этой оси на 2/3 единицы и сдвинутую по направлению оси ординат на 2 единицы.

График функции

Давайте разберемся в этих геометрических преобразованиях графика функции пошагово на конкретных примерах. С помощью геометрических преобразований графика функции f(x) может быть построен график любой функции вида ±k₁·f(±k₂((x+a))+b, где - k₁>0, k₂>0 коэффициенты сжатия (при 0<k₁<1, 0<k₂<1) или растяжения (при k₁>1, k₂>1) вдоль осей oy и ox соответственно, знаки "минус" перед коэффициентами k₁ и k₂ указывают на симметричное отображение графика относительно координатных осей, а и b определяют сдвиг относительно осей абсцисс и ординат соответственно.

Геометрические преобразования графика функции:

Первый вид - масштабирование (сжатие или растяжение) вдоль осей абсцисс и ординат.
На необходимость масштабирования указывают коэффициенты  k₁ и k₂ отличные от единицы, если 0<k₁<1, 0<k₂<1, то происходит сжатие графика относительно oy и растяжение относительно ox, если k₁>1, k₂>1, то производим растяжение вдоль оси ординат и сжатие вдоль оси абсцисс.

Второй вид - симметричное (зеркальное) отображение относительно координатных осей.
На необходимость этого преобразования указывают знаки "минус" перед коэффициентами k₁ (в этом случае симметрично отображаем график относительно оси ox ) и k₂ (в этом случае симметрично отображаем график относительно оси oy). Если знаков "минус" нет, то этот шаг пропускается.

Третий вид - параллельный перенос (сдвиг) вдоль осей ox и oy.

Это преобразование производится в последнюю очередь при наличии коэффициентов a и b, отличных от нуля. При положительном а график сдвигается влево на |а| единиц, при отрицательных а – вправо на |а| единиц. При положительном b график функции параллельно переносим вверх на |b| единиц, при отрицательном b – вниз на |b| единиц.

Задания для практического занятия

Подготовка к работе на заняти:

• настрой на работу, организация внимания;
• проверка домашнего задания
• актуализация опорных знаний. Повторение понятий: числовая функция, область определения функции, область значения функции, аргумент функции.

Задание 1
1) Графики, каких функций Вы знаете?
Ответ: Графики линейной функции, квадратичной функции, обратной пропорциональности, тригонометрических функций.

Какие функции записаны на доске?

y = kx+b, y = ax²+bx+c, y = k/x, y = sin x, y = tg x, y = x³
Ответ: линейная, квадратичная, обратная пропорциональность, тригонометрические (синус, тангенс), кубическая.
2) Что является графиком указанных функций:

y = kx+b, y = ax²+bx+c, y = k/x, y = sin x, y = tg x, y = x³

Ответ: графиком функции является: прямая, парабола, гипербола, синусоида, тангенсоида, кубическая парабола.

Задание 2

(Устно)
Построим график функции: y = -x²+2 и y = 1/2 x²
Устно разбираем последовательность преобразований, а преподаватель фиксирует ее на доске.

Задание 3
Построить графики функций. Выполнение задания у доски с консультацией преподавателя. Работа с конспектом.
а) у = х/(х + 2)

б) у = | х2 + х | - 2
Задание 4

Работа с конспектом и по учебнику стр .69 - 71. Используя способы сдвига, растяжения и сжатия построить графики функций и записать из свойства.
Работа у доски с консультацией преподавателя: № 180 (2, 3); 185 (1, 4);

Задание 5
Сделать самостоятельно № 186 (1, 3).

Задание 6

Проверочная работа на тему "Функции. Их свойства и графики"

(все задания выполнены на карточках-распечатках)

I вариант

1) Постройте графики функций:
а) у = (x-4)²

б) у = 1/2(x+2)²

2) Пусть дан график функции y=f(x). Как получить график функции y = f(x+3)-4?

3) Постройте графики функций,
а) у = (1/x+3)-4

б) у = (x+3)²-4

II вариант

1) Постройте графики функций:
а) у = 2(x-1)²

б) у = -(x+3)²

2) Пусть дан график функции y=f(x). Как получить график функции y = f(x-5)+2?

3) Постройте графики функций:
а) у = (1/x-5)+2

б) у =(x-5)² + 2

III вариант

1) Постройте графики функций:
а) у = -0,5(x-4)²

б) у = (2x-3)²

2) Пусть дан график функции y = f(x). Как получить график функции y = f(x+1)+3?
3) Постройте графики функций:
а) у = (1/x+1)+3

б) у = (x+1)² + 3

IV вариант

1) Постройте графики функций:
а) у = 4x²+4х+1

б) у = - (x²/4) -х-1

2) Пусть дан график функции y=f(x). Как получить график функции y = f(x-2)-1?

3) Постройте графики функций:
а) у = (1/x-2)-1

б) у = (x-2)² -1
В конце занятия обсуждение, выставление оценок.

Итог

Подвести итог работы на занятии. Записать домашнее задание.

Вопросы для закрепления теоретического материала к практическому занятию:

1. Какие функции называются элементарными?
2. Какие функции называются ограниченными снизу/сверху?
3. Как построить график функции способом растяжения/сжатия?
4. Как построить график функции способом сдвига по оси?
5. Что такое симметричное отображение графика?
6. Как построить график функции, содержащий модуль?