Домашняя контрольная работа по математике на тему "Степенная функция. Сложная и обратная функции"

Цель:

• Обучающая: повторить и систематизировать знания по теме «степенная функция». Проверить усвоение учащимися изученного материала: умения распознавать сложные функции, строить графики сложных функций.
• Развивающая: формирование абстрактного мышления и воспитание математической культуры.
• Воспитательная: показать значимость изучаемой темы в разделе математика.

Вариант 1

1. Работа с графиком

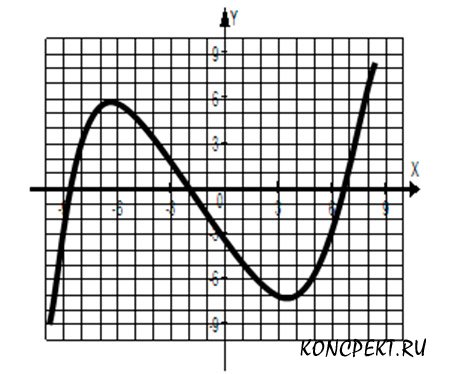
1.1. По графику функции y=f(x), изображенному на рисунке, определите промежуток убывания функции:
1.2 (-∞;5]; 2.(-6;4); 3. [-6;4]; 4. [4;∞).

1.3 По графику функции y=f(x), изображенному на рисунке, определить максимум и минимум функции.

1.4 По графику функции y=f(x), изображенному на рисунке указать область определения и область значения функции. По графику функции y=f(x), изображенному на рисунке, указать промежутки, где f(x)>0.

2. Найти область определения функции y=√(x-4).
1. [4;∞);   2. (4;∞); 3. (-∞;-4]; 4. (-∞;4)

3. Укажите наибольшее значение функции y=2x-10 на отрезке [-1;2].
1. -12; 2. 8; 3. -6; 4. -2.

4. При каких значениях x функция y=2x-4 принимает положительные значения?

1. [-2;∞); 2. (2;∞); 3. (-∞;0,5); 4. (-∞;-2]

5. Найдите нули функции y=x²+2x.
1. {-1; -2}; 2. {0} ; 3. {0;2}; 4. {0;-2}.

6. Постройте график функции: y=(x-2)²+3

Вариант 2

1. Работа с графиком

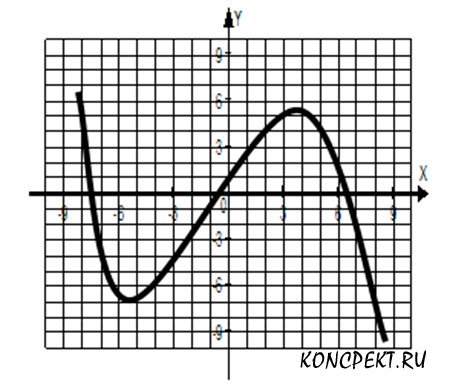
1.1 По графику функции y=f(x), изображенному на рисунке, определите промежуток возрастания функции.
1. (-∞;4]; 2. [-5;4]; 3. (-5;4); 4. [4;∞)

1.2 По графику функции y=f(x), изображенному на рисунке, определить максимум и минимум функции.
1.3 По графику функции y=f(x), изображенному на рисунке указать область определения и область значения функции.
1.4 По графику функции y=f(x), изображенному на рисунке, указать промежутки, где f(x)>0.

2. Найти область определения функции y=5/(x+4).
1. (-∞;-4)⋃(-4;∞); 2. (-4;∞); 3. [4; ∞); 4. (-∞;-4]⋃[4; ∞).

3. Укажите наименьшее значение функции y=2/(х+2) на отрезке [0;2].
1. -1; 2. -1/2; 3. 1; 4. 0,5.

4. При каких значениях x функция y=3x+6 принимает отрицательные значения?
1. (-2; ∞); 2. [2; ∞); 3. (-∞; -2); 4. (-∞;-2]

5. Найдите нули функции y=(3x-x)².
1. {-1; 3}; 2. {0; -3}; 3. {0}; 4. {0;3}.

6. Постройте график функции: y=(x+2)²+1.