Применение информационных технологий в процессе преподавания финансовой математики и статистики

Сегодня нельзя всерьез претендовать на работу экономиста, менеджера, бухгалтера, финансиста, специалиста по ценным бумагам и т.п., если не уметь обращаться с компьютером. Умение работы с компьютером предполагает прежде всего знание текстовых процессоров, электронных таблиц, системы управления базами данных и систем для работы с графикой.

Excel является одной из самых популярных программ работающих в операционной среде Windows, поскольку объединяет возможности графического и текстового редактора с мощной математической поддержкой, на базе Excel созданы многие бухгалтерские и банковские

Функции Excel используют базовые модели финансовых операций, базирующиеся на математическом аппарате методов финансово-экономических расчетов. Использование возможностей компьютера и табличного процессора Excel позволяет облегчить выполнение расчетов и представить их в удобной для пользователя форме.

Рассмотрим специфику задания значений аргументов финансовых функций

1. Все аргументы, означающие расходы денежных средств (например, ежегодные платежи), представляются отрицательными числами, а аргументы, означающие поступления (например, дивиденды), представляются положительными числами.
2. Все даты как аргументы функции имеют числовой формат представления.
3. При вводе аргумента типа дата непосредственно в поле ввода Мастера функции можно воспользоваться встроенной функцией ДАТА, которая осуществляет преобразование строки символов в дату. Для этого нажимается кнопка вызова Мастера функций, находящаяся перед полем, и выбирается функция категории Дата и время — ДАТА. Далее заполняется экран ввода.
4. При непосредственном вводе формулы в ячейку необходимо следить за тем, чтобы каждый аргумент находился строго на своем месте. Если какие-то аргументы не используются, то необходимо поставить соответствующее число разделительных знаков.

Excel предлагает следующие финансовые функции для расчета операций по кредитам и займам:

• определение будущей стоимости на основе постоянной процентной ставки: БС;
• определение будущей стоимости на основе переменной процентной ставки: БЗРАСПИС;
• определение текущей стоимости: ПС, ЧПС, ЧИСТНЗ;
• определение срока платежа и процентной ставки: КПЕР, СТАВКА;
• расчет эффективной и номинальной ставки процентов: ЭФФЕКТ, НОМИНАЛ;
• расчет постоянных периодических выплат: ПЛТ;
• расчет платежей по процентам: ПРОЦПЛАТ;
• расчет платежей по процентам по займу: ОБЩПЛАТ
• расчет основных платежей по займу: ОСПЛТ
• расчет суммы основных выплат по займу: ОБЩДОХОД
• определение скорости оборота инвестиций: ЧИСТВНДОХ, ВСД
• оценка инвестиций: ЧПС.

Финансовые функции Excel позволяют в считанные секунды построить график аннуитетных платежей, построение которого с помощью обычного калькулятора занимает много времени, что мешает студентам воспринять учебный материал.

• Рассмотрение отдельных тем по статистике требует изучения и применения следующих статистических функций:
• для расчета коэффициента корреляции: КОРРЕЛ;
• для построения линейного уравнения регрессии и оценки его значимости: РЕГРЕССИЯ.
• Для расчета дисперсии, моды и медианы - соответствующие функции;
• Функция ТЕНДЕНЦИЯ позволяет сделать прогноз на основе значений ряда динамики.

Рассмотрим на примерах применение некоторых функций.

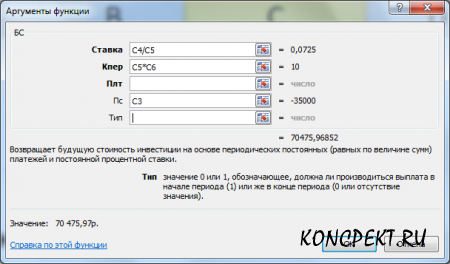
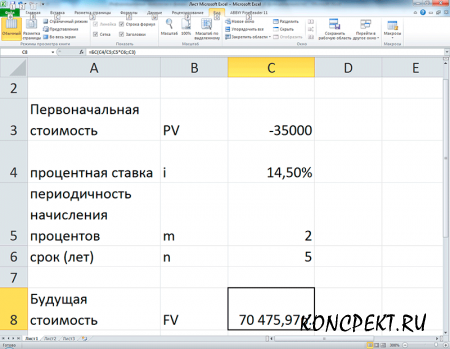
Пример 1. Рассчитаем, какая сумма окажется на счете, если 27000. руб. положены на 33 года под 13,5% годовых. Проценты начисляются каждые полгода.

Решение:
Для расчета применяется формула:

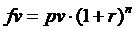
т.к. требуется найти будущее значение единой суммы вклада. В условии задачи указан годовой процент и число лет. Если проценты начисляются несколько раз в год, то необходимо рассчитать общее количество периодов начисления процентов и ставку процента за период начисления.

Используя функцию БС, получим: БС(13,5%/2, 33*2,,-27000) = 2012,07

Первоначальная сумма вводится со знаком "минус".
Для сравнения проведем расчет по формуле:

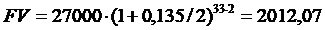
Удобно в данном случае составить электронную таблицу, используемую как шаблон.

Ввод формул

Результат расчета

Аннуитетный платеж - это равный по сумме ежемесячный платеж по кредиту, который включает в себя сумму начисленных процентов за кредит и сумму основного долга.
Величина аннуитетного платежа вычисляется по формуле: Y_t=Dq/1-(1+q)^-n

где: Yt - величина срочной уплаты;
D - первоначальная сумма долга;
q - процентная ставка на сумму долга;
n - срок долга в годах;
t - номер года, t = 1, 2, …, n.

Альтернативный расчет предполагает использование функций Excel. Функции EXCEL позволяют вычислять следующие величины, связанные с периодическими выплатами:

1. периодические платежи, осуществляемые на основе постоянной процентной ставки и не меняющиеся за все время расчета (функция ПЛТ);
2. платежи по процентам за конкретный период (функция ПРПЛТ);
3. сумму платежей по процентам за несколько периодов, идущих подряд (функция ОБЩПЛАТ);
4. основные платежи по займу (за вычетом процентов) за конкретный период (функция ОСПЛТ);
5. сумму основных платежей за несколько периодов, идущих подряд (функция ОБШДОХОД).

Все эти величины вычисляются, при расчете схемы равномерного погашения займа. Допустим, что заем погашается одинаковыми платежами в конце каждого расчетного периода. Будущая стоимость этих платежей будет равна сумме займа с начисленными процентами к концу последнего расчетного периода, если в нем предполагается полное погашение займа.

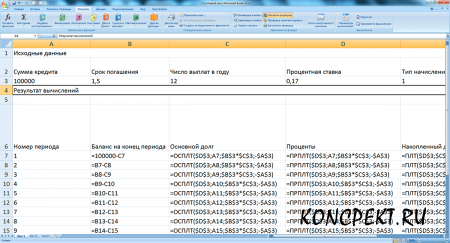
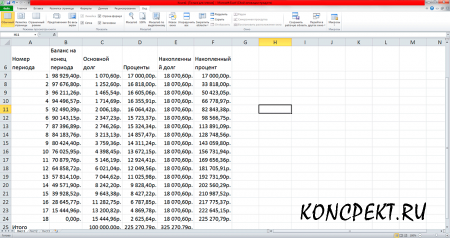
Пример 2. Сумма кредита 100000 руб., срок кредита 1,5 года ,процентная ставка 17 % годовых, выплаты осуществляются ежемесячно. Ввод формул представлен на рисунке 3, а результат расчетов - на рисунке 4.

Ввод формул при составлении графика погашения финансового долга аннуитетными платежами

График погашения кредита аннуитетными платежами

С целью минимизации "ручного" труда, студентам разъясняются возможности статистических финансовых функций, позволяющих ускорить расчеты, и тем самым повысить плотность урока.

При изучении темы "Статистическое изучение связей между явлениями" для построения уравнения регрессии и оценки его значимости, параллельно с традиционной подачей темы можно использовать финансовые функции, представленные в примере ниже.

Пример 3. По территориям региона приводятся данные за год, представленные в таблице.

1. Построить линейное уравнение парной регрессии y от x.
2. Рассчитать линейный коэффициент парной корреляции и среднюю ошибку аппроксимации.
3. Оценить статистическую значимость параметров регрессии и корреляции с помощью F-критерия Фишера и t-критерия Стьюдента.

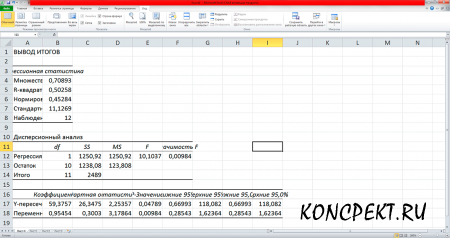
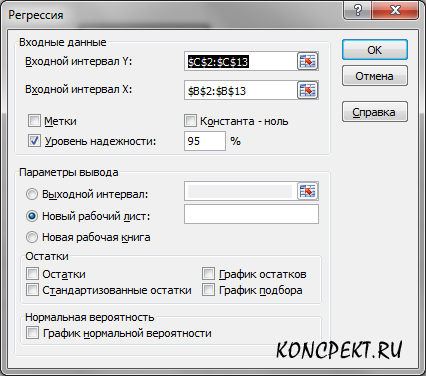
Для решения воспользуемся вставкой "Данные" - "Анализ данных" - "Регрессия" (ввод данных представлен на рисунках 4, 5. На рисунке 6 представлен результат статистического анализа, выполненного в Excel.

Результаты расчета

тогда уравнение регрессии имеет вид: У_x = 59,375+0,9545x

Полученное значение коэффициента корреляции свидетельствует о том, что связь между признаками прямая (так как значение коэффициента положительное) и тесная, так как r превышает 0,7 (составила 0,70893). С увеличением х увеличивается у.