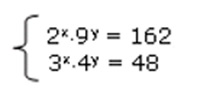Домашняя контрольная работа по математике на тему "Показательные функции. Свойства функций"

Учебные задачи:

• способствовать выработке навыка решения показательных уравнений и неравенств;
• обобщить методы и этапы решения показательных неравенств и систем показательных неравенств, формировать практические навыки их решения;
• формирование практических умений и навыков построения и чтения графиков функций.

Вопросы для закрепления теоретического материала к практическому занятию:

1. Какие неравенства называются показательными
2. Что такое область определения функции?
3. Какие характеристики показательной функции вы знаете?
4. Дайте определение возрастающей функции?
5. Дайте определение убывающей функции?
6. При каком условии показательная функция является возрастающей?
7. При каком условии показательная функция является убывающей?
8. Какие свойства у функции при a > 1 и при 0 < a < 1?

Задания к контрольной работе на тему "Показательные функции. Свойства функций"

Вариант I

1. Продолжите: Показательным уравнением называется уравнение…

2. Какое свойство показательной функции используется при решении неравенств? Сформулируйте его.

3. График функции ƒ(x) = 4^x расположен ниже графика функции g(x) = 16 при x<2. Объясните почему.

4. Решите неравенство (решение полностью обоснуйте)

3^4x+3 ≤ (1/9)^x2/2

5. Решите неравенства:

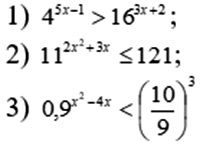
6. Решите систему неравенств:

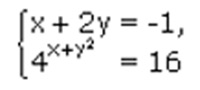
Вариант II

1. Продолжите: Показательным неравенством называется неравенство…

2. Какое свойство используется при решении показательных уравнений? Сформулируйте его.

3. График функции ƒ(x) = 0,3^x расположен ниже графика функции g(x) = 0,027 при x<3. Объясните почему.

4. Решите неравенство (решение полностью обоснуйте)

5. Решите неравенства:

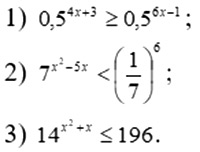
6. Решите систему неравенств: