Домашняя контрольная работа по математике на тему "Показательные уравнения и системы показательных уравнений"

Учебная цель:

• изучение основных методов решения показательных уравнений;
• формирование навыков решения показательных уравнений;
• развитие мыслительной деятельности, математической речи, потребности к самообразованию, творческой деятельности учащихся, умения находить наиболее рациональный способ решения.

Учебные задачи:

• способствовать выработке навыка решения показательных уравнений;
• обобщить методы и этапы решения показательных уравнений и систем показательных уравнений; формировать практические навыки их решения.
• формирование практических умений и навыков построения и чтения графиков функций.

Студент должен

уметь:

• находить значения степени;
• отличать показательное уравнение от других
• решать показательные уравнения различными методами;
• строить графики показательной функции;
• преобразовывать числовые и буквенные выражения, содержащие степени.

знать:

• способы решения показательных уравнений;
• свойства показательной функции;
• решение систем уравнений;
• использование свойств графиков для решения уравнений и систем уравнений.

Задания для практического занятия:

Повторение понятий степень с рациональным и действительным показателем.

Решить самостоятельно:

1. 3^х=9

2. (1/9)^х=1

3. 0,5^х=0,125

4. 10^х=∜1000

5. 5^х=1/∛25

6. (2/3)^х∙(9/8)^х=27/64

7. (5^{(х^(2+х-2)})^(3-х)=1

8. 2^(х+1)=4

9. 5^(3х-1)=0,2

10. 6^(2х-8)=216^х

Проверочная работа на тему "Показательные уравнения и системы показательных уравнений"

(все задания выполнены на карточках-распечатках)

I вариант

1. Контрольные вопросы
а) указать свойства показательной функции;
б) привести примеры возрастающей и убывающей показательной функции.

2. Решите уравнения:

8^x = 64

2^x+1 = 32

7^x = 1/343

(4/5)^x = 25/16

3^-1-x = (1/3)^2x+3

3^2x - 6 x 3^x - 27 = 0
Решите систему уравнений:

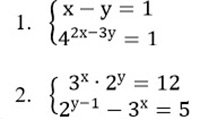
II вариант

1. Контрольные вопросы
а) указать свойства показательной функции;
б) привести примеры возрастающей и убывающей показательной функции.

2. Решите уравнения:

0,5^x = 0,125

3^x-2 = 81

(1/6)^x = 36

(3/2)^x = 16/81

(1/6)^4x-7 = 6^x-3

2^2x - 6 x 2^x + 8 = 0

Решите системы уравнений:

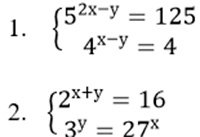
В конце занятия преподаватель каждой группе раздает карточки с ответами. Обсуждение. Выставление оценок.

Вопросы для закрепления теоретического материала к практическому занятию:

1. Какие уравнения называются показательными?
2. Какие способы решения показательных уравнений вы знаете?
   а) приведение степеней в левой и правой частях уравнения к одному основанию;
   б) разложение частей уравнения на множители;
   в) введение новой переменной;
   г) графический способ решения;
   д) деление на степень;
   е) оценивание значения левой и правой частей уравнения с помощью свойств показательной функции, подбор корня.
3. Какие характеристики функции вы знаете?
4. Что такое область определения функции?
5. Какова область определения показательной функции
6. Какими свойствами может обладать показательная функция?
7. Какие функции называются монотонными?
8. Дайте определение возрастающей функции?
9. Дайте определение убывающей функции?
10. При каком условии показательная функция является возрастающей?
11. При каком условии показательная функция является убывающей?