Практическая работа по алгебре на тему "Сложная и обратная функции"

Раздел: Функции, их свойства и графики.

Учебная цель: познакомиться с взаимно обратными функциями, изучить условия существования обратной функции и ее свойства, научиться строить графики обратных функций.

Учебные задачи:

• формировать знания по новой теме в соответствии с программным материалом;
• изучить свойство обратимости функции и научить находить функцию, обратную данной;
• овладеть понятием обратная функция и усвоить методы нахождения обратной функции
• активизировать интерес к получению новых знаний, воспитание графической культуры, формирование точности и аккуратности при выполнении чертежей.

Образовательные результаты, заявленные в ФГОС:

Учащийся должен

уметь:

• задавать функцию обратную данной формулой,
• находить область определения и множество значений функции обратной к данной;
• строить графики обратных функций.

знать:

• понятие обратной функции;
• алгоритм задания функции обратной данной формулой;
• свойство графиков взаимно обратных функций.

Оборудование: рабочая тетрадь в клетку, раздаточные материалы (карточки-задания, по количеству обучающихся), калькулятор, ручка, карандаш.

Краткие теоретические и учебно-методические материалы по теме практической работы

Взаимно обратные функции

Пусть дана функция у = f(x). Она имеет обратную, если из зависимости у = f(x) можно переменную х однозначно выразить через переменную у. Выразив х через у, мы получим равенство вида х = g(y). В этой записи g обозначает функцию, обратную к f.

Если функция g является обратной для функции f, то и функция является обратной для функции g. Пару функций f и g называют взаимно обратными функциями.

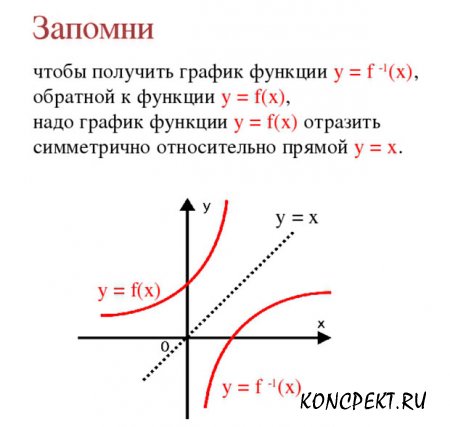
График обратной функции

Если мы одновременно построим графики функций f и g в одной и той же системе координат, откладывая по оси абсцисс аргументы обеих функций, а по оси ординат – их значения, то эти графики будут симметричны друг другу относительно прямой у = х.

Построение графика обратной функции

Свойства взаимно обратных функций

Отметим некоторые свойства взаимно обратных функций:

1. Тождества. Пусть f и g – взаимно обратные функции. Тогда : f(g(y)) = у и g(f(x)) = х.
2. Область определения. Пусть f и g – взаимно обратные функции. Область определения функции f совпадает с областью значений функции g, и наоборот, область значений функции f совпадает с областью определения функции g.
3. Монотонность. Если одна из взаимно обратных функций возрастает, то и другая возрастает. Аналогичное утверждение верно и для убывающих функций.
4. Графики. Графики взаимно обратных функций, построенные в одной и той же системе координат симметричны друг другу относительно прямой у = х.

Задания для практического занятия

Подготовка к работе на занятии:

• настрой на работу, организация внимания;
• проверка домашнего задания.

Задание 1

(Устно)
а) Какие из функций: У=2х+3; у=3х-1; у=-х2+3; у=х3; у= х4 не имеют обратных функций?
б) Вопрос. Сформулируйте условие существования функции, обратной данной.

Задание 2

Функция g(x) – обратная функции f(x). D(f) = [2; +∞), E(f) = (-∞; 3). Найти D(g), E(g).
Вопрос: Что можно сказать о графиках взаимно обратных функций?

Задание 3

§7, Стр. 47. Работа по учебнику:

а) Прочитать материал до задачи 2. Повторить определения. Вспомнить, какие функции называются обратимыми, какие обратными.
б) Разобрать задачу 1. Записать ее в тетрадь.

Вспомнить какие функции называют взаимно обратными, какие монотонными. Разобрать задачу 2. Записать ее в тетрадь.

Задание 4
§7, стр. 50. Работа по учебнику:

а) Прочитать материал стр. 50-51. Повторить теорему об обратимости функции и теорему о симметричности графиков функций.
б) Обсудить рис. 18 и рис. 19. Сделать вывод. Записать его в тетрадь.

Задание 5

Устно фронтальный опрос делаем № 131 (весь). Определить по графику, обратима ли данная функция? Ответить на вопросы преподавателя, обсудить ответы.

Задание 6

Работа у доски с консультацией преподавателя:
№132 (1, 2); 133 (1); 134 (а); 136 (1); 137 (1).

Задание 7

Сделать самостоятельно № 132 (3, 4); 133 (2); 134 (б, в); 13 6(2); 137 (4, 5).
Обсудить и проверить решения друг с другом. Дополнительно (индивидуально) тем, кто быстрее справится с заданиями: № 186 (1, 3). Обсудить и проверить решения друг с другом.

Подведение итогов

Подвести итог работы на занятии. Записать домашнее задание.

Вопросы для закрепления теоретического материала к практическому занятию:

1. Какая функция называется обратимой?
2. Любая ли функция обратима?
3. Какая функция называется обратной данной?
4. Как связаны область определения и множество значений функции и обратной ей функции?
5. Если функция задана аналитически, как задать формулой обратную функцию?
6. Если функция задана графически, как построить график обратной ей функции?
7. Что можно сказать о графиках взаимно обратных функций?
8. Какие функции называются монотонными?
9. Какая функция является обратной к степенной функции y = xp?