Практическое занятие по геометрии на тему "Нахождение углов между прямой и плоскостью. Использование признака перпендикулярности плоскостей"

Учебная цель: формировать пространственное мышление; систематизировать знания по теме.

Учебные задачи:

• обобщить, систематизировать и закрепить полученные знания на предыдущих уроках:
• проверить свои знания теории при решении задач.

Краткие теоретические и учебно-методические материалы по теме практической работы

Определения перпендикулярности прямых в пространстве

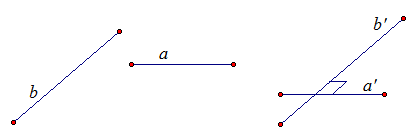
Две прямые называются перпендикулярными, если угол между ними равен 90°

Лемма

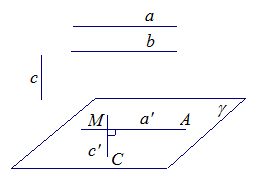
Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к этой прямой.

Определение перпендикулярности прямой и плоскости

 

Прямая называется перпендикулярной к плоскости, если она перпендику-лярна к любой прямой, лежащей в этой плоскости

Обозначение: a ⊥ α

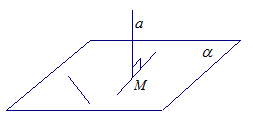
Свойство

Если a ⊥ α, то a ∩ α = M. (пересечение а и )
Доказательство:

Прямая и плоскость или пересекаются в одной точке, или параллельны, или прямая лежит в плоскости.

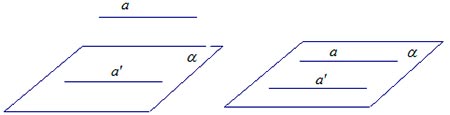
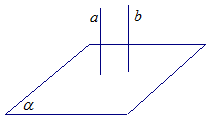
Теорема
Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перепедикуляная к этой плоскости.

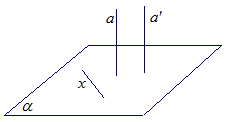
Обратная теорема
Если две прямые перпендикулярны к плоскости, то они параллельны.

Задача 1
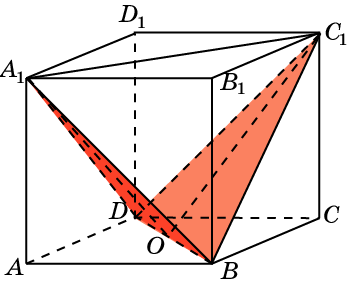
Дан параллелепипед ABCDA₁B₁C₁D₁. Докажите, что DC⊥B₁C₁ и AB⊥A₁D₁, и ∠BAD = 90º если:

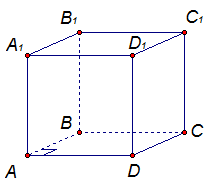
Доказательство:
ABCD – прямоугольник, так как в параллелограмме ABCD угол ∠BAD = 90º.
Прямая В₁С₁ параллельна прямой ВС, а прямая ВС перпендикулярна прямой DС. Значит, по лемме, прямая DС перпендикулярна В₁С₁.
Прямая АВ перпендикулярна прямой ВС, а ВС параллельна прямой A₁D₁. Значит, по лемме, прямая АВ перпендикулярна A₁D₁. Задача доказана.
Рассмотрим другое доказательство факта, что DC⊥B₁C₁.
Угол DCB равен углу между прямыми DC и В₁С₁. Угол DCB – прямой. Значит, прямые DС и В₁С₁ перпендикулярны.

Задача 2
В тетраэдре ABCD - BC⊥AD. Докажите, что AD⊥MN, где М и N середины ребер АВ и АС.

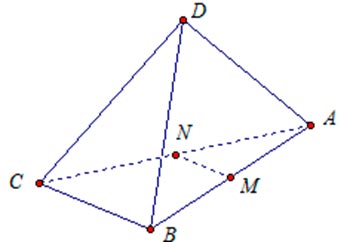
Доказательство:
MN – средняя линия треугольника АВС. По свойству средней линии, ВС параллельна MN.
Прямые ВС и MN параллельны, а прямые ВС и AD перпендикулярны. Значит, по лемме, прямые AD и MN перпендикулярны, что и требовалось доказать.

Задания для практического занятия

Задание 1
подготовка к работе на занятии:

• настрой на работу, организация внимания;
• проверка домашнего задания;
• актуализация опорных знаний.

Задание 2
Фронтально с группой:

Закончить предложение:
а) две прямые в пространстве называются перпендикулярными, если… (угол между ними равен 90°)
б) прямая называется перпендикулярной к плоскости, если… (она перпендикулярна к любой прямой, лежащей в этой плоскости)
в) если две прямые перпендикулярны к плоскости, то они… (параллельны)
г) если плоскость перпендикулярна к одной из двух параллельных прямых, то она… (перпендикулярна и к другой прямой)
д) если две плоскости перпендикулярны к одной прямой, то они… (параллельны)

Задание 3
Глава 2, §1, Стр. 34 Л.С. Атанасян и др., Геометрия. 10-11 кл. – М.: Просвещение, 2014.

Работа по учебнику.
а) Прочитать материал стр. 34-38. Записать основные определения себе в тетрадь.

Работа в парах. Вопросы друг другу и преподавателю.
а) Лемма стр. 34 разобрать у доски. Обсуждение. Записать в тетрадь.
б) Теорема стр. 35 разобрать у доски. Обсуждение. Записать в тетрадь.
в) Теорема стр. 36 разобрать у доски. Обсуждение. Записать в тетрадь.
г) Теорема стр. 38 разобрать у доски. Обсуждение. Записать в тетрадь.

Задание 4
Самостоятельно выполнить задания № 116. (с проверкой у доски – несколько человек)

Задание 5
Сделать самостоятельно № 117. Дополнительно (индивидуально) тем, кто быстрее справится с заданиями: № 119 (а). Обсудить и проверить решения друг с другом.

Задание 6
Глава 2, §2, Стр. 40 Л.С. Атанасян, Геометрия. 10-11 кл.

Работа по учебнику.
а) Прочитать материал стр. 40-44 Записать основные определения себе в тетрадь. Работа в парах. Вопросы друг другу и преподавателю.
б) Теорему о трех перпендикулярах стр. 42 разобрать у доски. Обсуждение. Записать в тетрадь.
в) Определение стр. 43 разобрать у доски. Обсуждение. Записать в тетрадь.

Задание 7

Самостоятельно выполнить задания № 149, 150. (с проверкой у доски – несколько человек)

Задание 8
Сделать самостоятельно № 154. Дополнительно (индивидуально) тем, кто быстрее справится с заданиями: № 162. Обсудить и проверить решения друг с другом.

Задание 9
Глава 2, §3, Стр. 47 Л.С. Атанасян и др., Геометрия. 10-11 кл.

Работа по учебнику.
а) Прочитать материал стр. 47-52. Записать основные определения себе в тетрадь.
Работа в парах. Вопросы друг другу и преподавателю.
б) Теорему стр. 49 разобрать у доски. Обсуждение. Записать в тетрадь.
в) Следствие из теоремы стр. 50 разобрать у доски. Обсуждение. Записать в тетрадь.
г) Теорему стр. 51 разобрать у доски. Обсуждение. Записать в тетрадь.
д) Следствие стр. 51 разобрать у доски. Обсуждение. Записать в тетрадь.

Задание 10
Самостоятельно выполнить задания № 170. (с проверкой у доски – несколько человек)

Задание 11
Сделать самостоятельно № 173. Разобрать задачу 362. Обсуждение. Дополнительно (индивидуально) тем, кто быстрее справится с заданиями: № 185. Обсудить и проверить решения друг с другом.

Проверочная работа по теме: "Прямые и плоскости в пространстве"

Вариант 1

1. Из вершины A квадрата ABCD перпендикулярно его плоскости проведен отрезок AK, равный 3. Из точки K опущены перпендикуляры на стороны BC и CD. Перпендикуляр из точки K к стороне BC равен 6. Найдите углы, которые образуют эти перпендикуляры с плоскостью квадрата.

2. В кубе A…D₁ найдите угол между прямой AA₁ и плоскостью AB₁C₁.

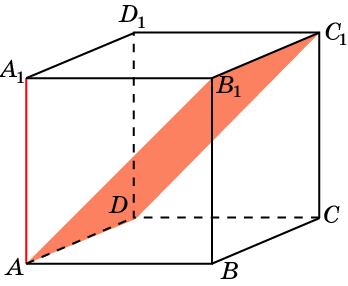
3. В кубе A…D₁ найдите угол между плоскостями ABC и CDD₁.

4. Из вершины A квадрата ABCD перпендикулярно его плоскости проведен отрезок AK, равный 3. Из точки K опущены перпендикуляры на стороны BC и CD. Перпендикуляр из точки K к стороне BC равен 6. Найдите углы, которые образуют эти перпендикуляры с плоскостью квадрата.

5. В кубе A…D₁ найдите угол между прямой AA₁ и плоскостью AB₁C₁.
6. В кубе A…D₁ найдите угол между плоскостями ABC и CDD₁.

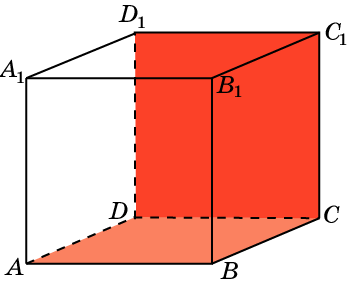
7. В кубе A…D₁ найдите угол между плоскостями ACC₁ и BDD₁.

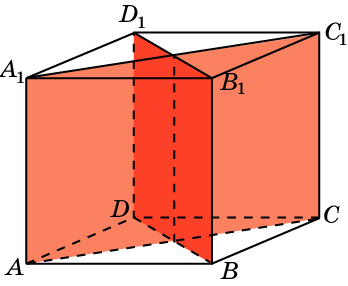
8. В кубе A…D₁ найдите угол между плоскостями ABC и BC₁D.

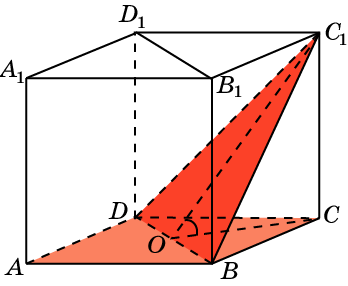
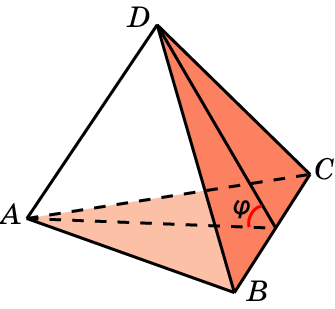
9. В тетраэдре ABCD, ребра которого равны 1, найдите угол между плоскостями ABC и BCD.

Вариант 2

1. Из вершины A квадрата ABCD перпендикулярно его плоскости проведен отрезок AK, равный 6. Из точки K опущены перпендикуляры на стороны BC и CD. Перпендикуляр из точки K к стороне BC равен 18. Найдите углы, которые образуют эти перпендикуляры с плоскостью квадрата.

2. В кубе A…D₁ найдите угол между прямой AB1 и плоскостью BCC₁.

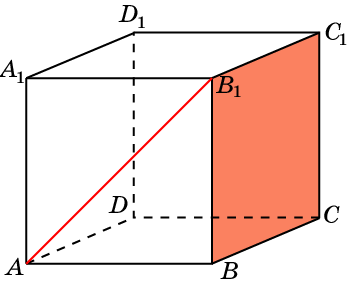
3. В кубе A…D₁ найдите угол между плоскостями ABC и CDA₁.

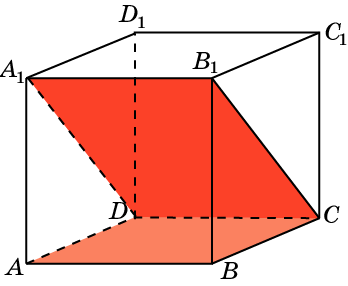
4. В кубе A…D¹ найдите угол между плоскостями ABC и BDD₁.

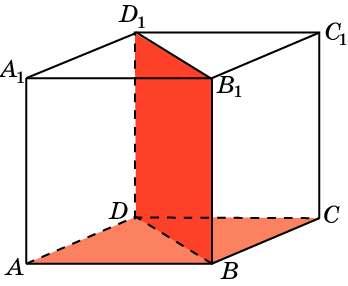
5. В кубе A…D₁ найдите угол между плоскостями BC₁D и BA₁D.

 

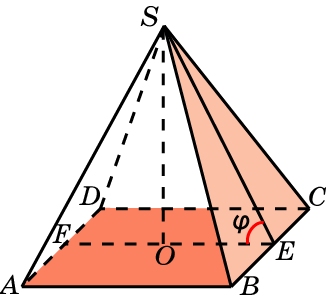
6. В правильной пирамиде SABCD, все ребра которой равны 1, найдите угол между плоскостями SBC и ABC.

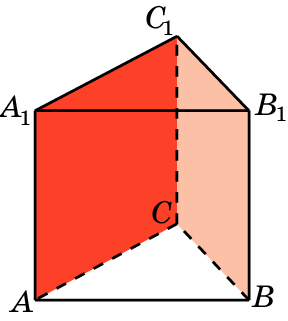
7. В правильной треугольной призме ABCA₁B₁C₁, все ребра которой равны 1, найдите угол между плоскостями ACC₁ и BCC₁.

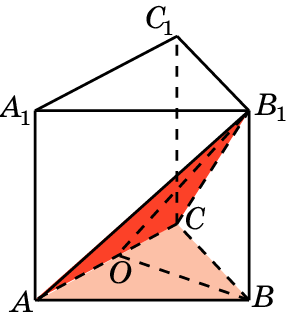
8. В правильной треугольной призме ABCA₁B₁C₁, все ребра которой равны 1, найдите угол между плоскостями ABC и ACB₁.

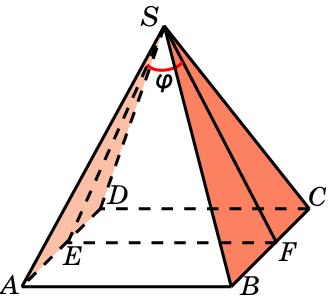
9. В правильной пирамиде SABCD, все ребра которой равны 1, найдите угол между плоскостями SAD и SBC.

Вопросы для закрепления теоретического материала к практическому занятию

1. Какие две плоскости называются перпендикулярными?
2. Какая прямая называется перпендикулярной к плоскости?
3. Что называется расстоянием от точки до плоскости?
4. Что называется расстоянием между параллельными плоскостями?
5. Что называется расстоянием между прямой и параллельной ей плоскостью?
6. Как измерить расстояние между скрещивающимися прямыми?
7. Что называют углом между прямой и плоскостью?
8. Что называется общим перпендикуляром двух скрещивающихся прямых?
9. Что называется расстоянием между двумя скрещивающимися прямыми?
10. Как измеряется двугранный угол?

perpendikulyarnost.rar

Размер:

202.48 Kb

Скачали:

22