Практическая работа по геометрии "Действия с векторами, нахождение элементов"

Раздел: Координаты и векторы.

Учебная цель: продолжить формирование знаний обучающихся по данной теме.

Задачи:

• Ввести определения вектора в пространстве, равенства векторов.
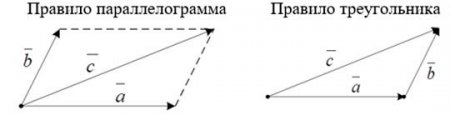
• Рассмотреть правила треугольника и параллелограмма сложения векторов в пространстве, правило вычитания векторов, правило сложения нескольких векторов в пространстве.

Обеспеченность занятия:

• Атанасян Л.С. Геометрия. 10-11 кл. – М.: Просвещение, 2014.
• Компьютер и мультимедийный проектор.
• Раздаточные материалы (карточки-задания, по количеству обучающихся).

Краткие теоретические и учебно-методические материалы по теме практической работы "Сложение векторов, умножение вектора на число"

В окружающем мире мы встречаемся с такими величинами, для которых важен не только размер, но и направление. Такими величинами являются, например, сила и скорость. В математике такие величины описываются векторами. 

Вектор – направленный отрезок.

Коллинеарными векторами называются такие векторы, которые лежат на параллельных прямых либо на одной прямой.

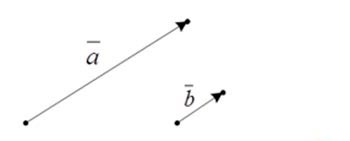
Умножением вектора на какое-либо число λ, можно растянуть или сжать вектор.

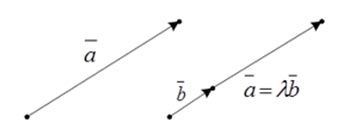
Если векторы коллинеарные и сонаправленные и их длины равны, то такие векторы называются равные.

Сложение векторов

Сложение векторов

Векторы в пространстве

Рассмотрим векторы в пространстве. Для этого необходимо выбрать три 

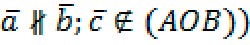
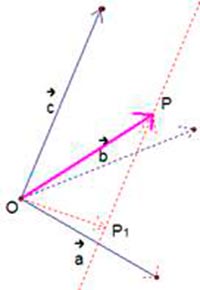
Теорема: в пространстве любой вектор можно разложить по трем данным некомпланарным векторам, причем коэффициенты разложения определяются однозначно: d = xa+yb+zc. То есть вектор d однозначно разлагается по векторам a, b, c с помощью чисел x, y, z (эта тройка чисел однозначная).

Понятие компланарности векторов

Векторы называются компланарными, если при откладывании их от одной и той же точки они будут лежать в одной плоскости.
Рассмотрим векторы:

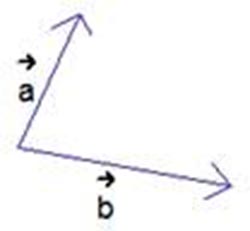
Мы знаем, что если заданы два неколлинеарных вектора на плоскости, то любой третий вектор на той же плоскости можно однозначно разложить по этим векторам.

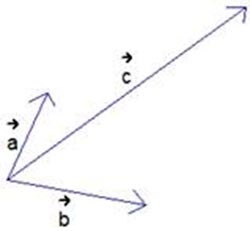
Теорема о разложении вектора по двум неколлинеарным

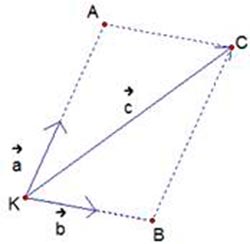
Теорема о компланарных векторах, сложение векторов в пространстве

Если вектор c можно представить в виде c=xa+yb, где х и у – конкретные числа, то вектора a, b и c компланарны.

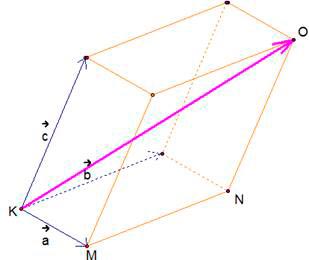
Теорема о разложении вектора по трем некомпланарным векторам

Любой вектор в пространстве можно разложить по трем заданным некомпланарным векторам, причем коэффициенты разложения определяются единственным образом: p=xa+yb+zc, где х, y, z – числа.

Задания для практического занятия

Задание 1

подготовка к работе на заняти:

• настрой на работу, организация внимания;
• проверка домашнего задания
• актуализация опорных знаний.

Задание 2

Фронтально с группой:

1. Как называются векторы, имеющие равные модули и противоположно направленные?

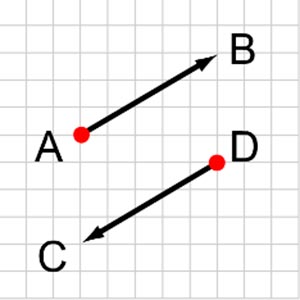
а) противоположные
б) противоположно направленные
в) равные

2. Тело переместили из точки А в точку В, а потом из точки В в точку С. Какой вектор представляет суммарное перемещение тела?

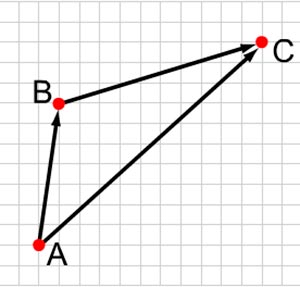
а) AB
б) BC
в) CA

3. Закончите предложение:

Суммой двух векторов называется вектор, построенный по правилу.... (треугольника)

4. Вставьте пропущенное слово:
Чтобы сложить два неколлинеарных вектора a и b, нужно отложить от произвольной точки О векторы OA=a и OB=b и построить .... ОАСВ, тогда OC= a+b (параллелограмм)

5. Изображенный на рисунке способ построения суммы нескольких векторов называется правилом... (многоугольника)

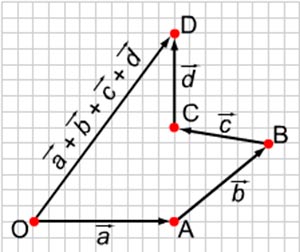
Задание 3

Глава 4, §1, Стр. 84 Л.С. Атанасян, Геометрия. 10-11 кл. – М.: Просвещение, 2014. (Учебники выдает преподаватель)

Работа по учебнику.
а) Прочитать материал стр. 84-85. Записать основные определения себе в тетрадь. Работа в парах. Вопросы друг другу и преподавателю.
б) Определение стр. 85 разобрать у доски. Обсуждение. Записать в тетрадь.

Задание 4
Самостоятельно выполнить задания № 320 (а), 322 (с проверкой у доски – несколько человек).

Задание 5
Сделать самостоятельно № 320 (б), 323

Дополнительно (индивидуально) тем, кто быстрее справится с заданиями: № 326. Обсудить и проверить решения друг с другом.

Задание 6
Глава 4, §2, Стр. 87 учебника Геометрия. 10-11 кл.

Работа по учебнику.
а) Прочитать материал стр. 87-89. Записать основные определения себе в тетрадь. Работа в парах. Вопросы друг другу и преподавателю.
б) Правила стр. 87 разобрать у доски. Обсуждение. Записать в тетрадь.
в) Правила стр. 88-89 разобрать у доски. Обсуждение. Записать в тетрадь.

Задание 7
Самостоятельно выполнить задания № 328 (а), 333 (а), 335(а) (с проверкой у доски – несколько человек)

Задание 8
Сделать самостоятельно № 328 б), 333 (б), 335 (б).

Дополнительно (индивидуально) тем, кто быстрее справится с заданиями № 347(а). Обсудить и проверить решения друг с другом.

Задание 9
Глава 4, §3, Стр. 92 учебника Геометрия. 10-11 кл.

Работа по учебнику.
а) Прочитать материал стр. 92-95. Записать основные определения себе в тетрадь.
Работа в парах. Вопросы друг другу и преподавателю.
б) Правила стр. 93 разобрать у доски. Обсуждение. Записать в тетрадь.
в) Теорему стр.94 разобрать у доски. Обсуждение. Записать в тетрадь.

Задание 10
Самостоятельно выполнить задания № 355 (а, б); 358 (а, б); 359 (а) (с проверкой у доски – несколько человек)

Задание 11
Сделать самостоятельно № 355(в), 358 (в), 359 (б).

Разобрать задачу 362. Обсуждение.
Дополнительно (индивидуально) тем, кто быстрее справится с заданиями: № 376 (а). Обсудить и проверить решения друг с другом.

Задание 12
Подвести итог работы на занятии. Записать домашнее задание.

Вопросы для закрепления теоретического материала к практическому занятию

1. Что называется направленным отрезком? Начало, конец, длина направленного отрезка?
2. Что называется вектором? Их обозначение.
3. Что называют длиной или модулем ненулевого вектора?
4. Что называют направлением ненулевого вектора?
5. Какой вектор называют единичным?
6. Какой вектор называют нулевым?
7. Какие векторы называют одинаково направленными, противоположно направленными?
8. Какие векторы называются коллинеарными?
9. Какие два вектора называются равными?
10. Какие векторы называются противоположными?
11. Что называется суммой двух векторов?
12. Правило треугольника.
13. Правило параллелограмма.
14. Правило многоугольника.
15. Правило параллелепипеда.
16. Что называется разностью двух векторов?