Рациональные приемы вычислений для повышения уровня вычислительных навыков

Устойчивый интерес к математическому образованию закладывается на этапе изучения математики в 5-7 классах, когда успешное освоение курса требует содержательного аппарата логического и алгебраического мышления.

Для успеха учащихся в изучении математики считаем важным безупречное овладение вычислительными навыками, которые совершенствуются на протяжении всех последующих лет обучения и применяются в рациональном решении различных задач.

Если ученик не умеет вычислять легко, то не сможет выполнять задания и не получит нужные баллы. За этим неуспехом последуют неуверенность, снижение самооценки, потеря мотивации к изучению предмета, тревожность. Поэтому так важно научить каждого ученика вычислять безошибочно.

Период овладения навыками зависит от индивидуальных способностей ребенка: одни будут "схватывать на лету", другие – через усердие, но будут тянуться "за лидерами" и добиваться успеха. Поэтому требуется адресный подход от учителя к ученику. Только при достижении верхней границы актуального уровня для ребенка открывается путь дальнейших успехов.

Одним из важных условий продуктивного урока считается включение в его начало упражнений устного счета. Это активизирует мышление, речь, моторику учащихся, готовит к восприятию абстрактных понятий. Отбор содержания и его объем зависят от ранее изученного материала и новой темы. Данный этап урока с четко обозначенными целями обеспечивает ближайшую перспективу.

Несмотря на цели изучения той или иной темы, связанные с отработкой определенных правил, там, где есть возможность, даем "пищу для ума", для поиска альтернативных решений. Тогда изучение становится не формальным, а осознанным. В отдельных случаях решение альтернативным способом может послужить проверкой ответа, полученного при традиционном изучении темы.

Математика, 6 класс, тема "Раскрытие скобок"

Пример 1.

Пункт 39 "Математика", № 352 (а, г, е), авторы Н.Я. Виленкин, В. И. Жохов и др.

Решите уравнение: а) 7,2 – (6,2 – x) = 2,2;

1 способ: по программе отрабатываем правило раскрытия скобок с учетом знака перед ними.

7,2 – 6,2 + х = 2,2; (Применяем правило раскрытия скобок, упрощаем)
1 + х = 2,2;
х = 2,2 – 1; (Ищем второе слагаемое, как компонент действия сложения)
х = 1,2.

2 способ: решаем через построение цепочки рассуждений.
7,2 – (6,2 – x) = 2,2;

х – неизвестное, значит, значение выражения 6,2 – x неизвестно. Демонстрируем, прикрывая выражение в скобках рукой, задаем вопрос: какое число надо вычесть из числа 7,2, чтобы получить 2,2?

Последует ответ: 5, записываем на доске вторую строчку решения уравнения: 6,2 – х = 5;
И снова вопрос: какое число надо вычесть из числа 6,2, чтобы получить 5? Ученики называют ответ, на доске записывается последняя строчка решения: х = 1,2.
Заметим, второй способ короче первого.

Пример 2.

г) (х + 3) – 17 = – 20;

1 способ: по программе отрабатываем правило раскрытия скобок с учетом знака перед ними.

х + 3 – 17 = – 20; (Применяем правило раскрытия скобок, упрощаем)
х – 14 = – 20;
х = – 20 + 14; (Ищем уменьшаемое, как компонент действия вычитания)
х = – 6.

2 способ: решаем через построение цепочки рассуждений.
(х + 3) – 17 = – 20;

Задаем вопрос: каким числом надо заменить выражение х + 3, чтобы равенство было верным? В отличие от уравнения под буквой а ситуация изменилась, поскольку вычитая 17, получается отрицательное число – 20.

Одни быстро сообразят, оперируя действием сложения чисел одного знака, и ответят: - 3. Другим, кто к этому моменту не вышел на верхнюю границу актуальной зоны в работе с положительными и отрицательными числами, может потребоваться помощь.

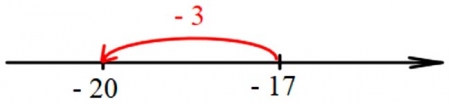
И здесь полезно построить рассуждение с помощью числовой прямой. По необходимости переформулировать вопрос: как из числа – 17 получить – 20?

Числовая прямая

Движение по числовой прямой влево, значит, - 17 уменьшаем на 3 единицы, поэтому значение выражения х + 3 равно – 3. Записываем: х + 3 = - 3;
И еще один вопрос, но опять в новой ситуации: с каким числом надо сложить 3, чтобы получить – 3? Учащиеся уже смелее называют ответ, записываем: х = - 6.

Работа публикуется в сокращении. Скачать полную версию материала вы можете по ссылке ниже