Из опыта работы: Применение образовательных технологий на уроках математики

Образовательные технологии – это совместная деятельность учащегося и педагога, это алгоритм действий педагога и детей в четко определенных условиях, который обеспечивает гарантированный образовательный результат.

Для достижения результата при планировании уроков я использую следующие технологии: карта понятий, карта памяти, фреймы (интеллект - карты). Эти технологии направлены на развитие умений анализировать, систематизировать информацию.

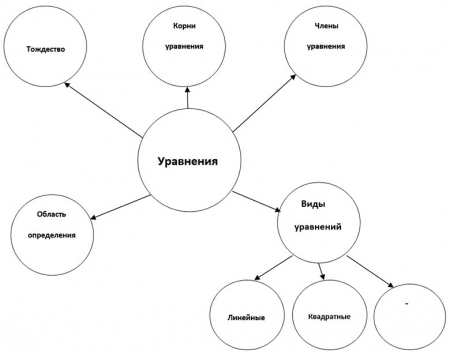
Карта понятий

Актуализация опорных знаний, умений и навыков – восполнить недостающие знания учащихся, вспомнить необходимые опорные знания.
Изображаем не схемы, а пишем слова.

Карта понятий

• Основная идея, проблема или слово располагается в центре.
• Главные ветви соединяются с центральной идеей, а ветви второго, третьего и т.д. порядка соединяются с главными ветвями.
• Над каждой линией – ветвью пишется только одно ключевое слово.

Данная технология позволяет эффективнее решать образовательные задачи:

1. поиск информации;
2. формирование понятий и установление связей между ними;
3. классификация, систематизация и обобщение.

Карта памяти

С помощью карт очень легко готовиться к экзаменам и зачетам. В своей работе использую прием "Разработка заданий массивом" из банка заданий для подготовки к ОГЭ.

Карта памяти:

• углубляет понимание;
• позволяет хранить информацию в свернутом виде, а при необходимости разворачивать;
• позволяет оценивать информацию с разных точек зрения и фиксировать ключевые моменты;
• помогает вспомнить детали, связанные с ключевыми моментами

Задание № 19 ОГЭ по математике "Анализ геометрических высказываний"

1. Укажите номера верных утверждений.

1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.

2) Вертикальные углы равны.

3) Любая биссектриса равнобедренного треугольника является его медианой

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.

Ответ: 1; 2.

2. Укажите номера верных утверждений.

1) Существует квадрат, который не является прямоугольником.

2) Если два угла треугольника равны, то равны и противолежащие им стороны.

3) Внутренние накрест лежащие углы, образованные двумя параллельными прямыми и секущей, равны.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
Ответ: 2; 3.

3. Укажите номера верных утверждений.

1) Биссектриса равнобедренного треугольника, проведенная из вершины, противолежащей основанию, делит основание на две равные части.

2) В любом прямоугольнике диагонали взаимно перпендикулярны.

3) Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
Ответ: 1; 3.

4. Укажите номера верных утверждений.

1) Центры вписанной и описанной окружностей равностороннего треугольника совпадают.

2) Существует квадрат, который не является ромбом.

3) Сумма углов любого треугольника равна 180° .

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
Ответ: 1; 3.

5. Укажите номера верных утверждений.

1) Если угол острый, то смежный с ним угол также является острым.

2) Диагонали квадрата взаимно перпендикулярны.

3) В плоскости все точки, равноудаленные от заданной точки, лежат на одной окружности.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
Ответ: 2; 3.

6. Укажите номера верных утверждений.

1) Если три стороны одного треугольника пропорциональны трем сторонам другого тре-угольника, то треугольники подобны.

2) Сумма смежных углов равна 180°.

3) Любая высота равнобедренного треугольника является его биссектрисой.

Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
Ответ: 1; 2.

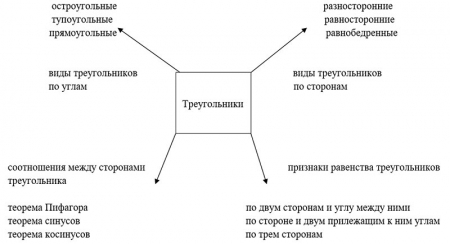
Фреймы (интеллект – карты)

Мыслим ассоциативно, выстраивая из полученной информации взаимосвязи мыслей и логическую структуру, а затем появляется образ.

Приемы работы

Обучающийся:

• отвечает на вопросы;
• формулирует вопросы;
• подписывает элементы в схеме;
• составляет связный текст по схеме.

Задания множественного выбора

Задания множественного выбора: "Есть"

1. геометрическая фигура;
2. четырехугольник;
3. прямоугольник;
4. ромб.

Задания множественного выбора: "Является"

1. геометрическая фигура;
2. четырехугольник;
3. прямоугольник;
4. трапеция.

Треугольники

Использование вышеперечисленных образовательных технологий позволяет мне повысить эффективность образовательного процесса, помогают достичь лучшего результата в обучении математике, повышают познавательный интерес к математике.