Лента Мебиуса глазами пятиклассников

В мире много удивительных и на первый взгляд обычных явлений и предметов. Со многими из них мы сталкиваемся в нашей повседневной жизни и совершенно не представляем, что за этим кроются удивительные знания и открытия.

Математика является одним из самых точных и удивительных предметов. Она лежит в основе музыки, спорта, архитектуры. Частно бывает, что для многих людей математика является трудной и непонятной, соответственно и неинтересной.

Однако, математика таит в себе много удивительных открытий. Одним из таких открытий является Лента Мебиуса.

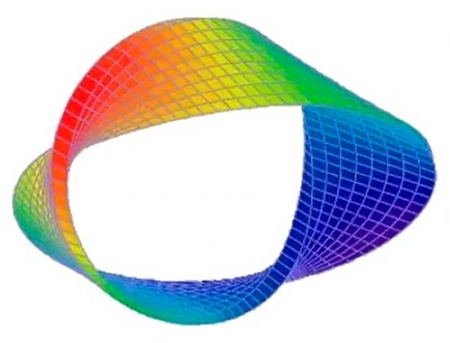
Лента Мебиуса – это поверхность, которая имеет только одну сторону и относится к "математическим неожиданностям"

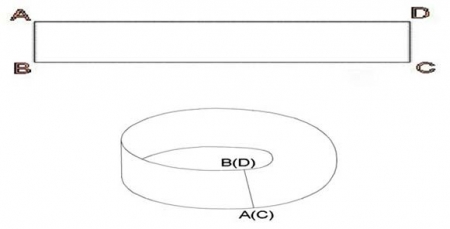
Для того, чтобы получить ленту Мебиуса, нужно взять бумажную ленту ABCD, концы AB и CD приложить друг к другу и перевернув один из концов на 180º склеить их. В результате получили лист (ленту) Мебиуса.

Изготовление ленты Мебиуса

На своих уроках я предлагаю ученикам разобраться в свойствах ленты Мебиуса.

Односторонность

Для подтверждения данного свойства проведем эксперимент. Нам понадобятся две одинаковые бумажные ленты. Одну склеим и получим обычное кольцо. Вторую изготовим согласно вышеизложенному способу, повернув один край ленты на 180 градусов относительно другого. Получим ленту Мебиуса.

Склеиваем две одинаковые бумажные ленты

Попробуем закрасить перекрученную ленту в два цвета – одним с внутренней стороны, а другим с внешней.

В результате проведенного эксперимента можно сделать вывод: у ленты Мебиуса только одна сторона.

Непрерывность

Для подтверждения данного свойства поставим точку на одной стороне каждого кольца (ленты Мебиуса и обычного кольца) и проведем непрерывную линию вдоль него, до тех пор, пока не вернемся снова в отмеченную точку.

Непрерывность ленты Мебиуса

Если на внешнюю сторону поставить паука, а на внутреннюю муху и разрешить им ползать, как угодно, но не переползая через край бумаги, то результат встречи пауки и мухи будет разным.

По результатам проведенных экспериментов, можно сделать вывод о том, что любая точка на листе Мебиуса может быть соединена с любой другой, не отрываясь от поверхности ленты.

Связность

Разрежем кольца вдоль пополам, по линии параллельной краям.

Разрежем кольца вдоль пополам

Данный эксперимент доказывает, что лист Мебиуса двусвязен, т.к. если разрезать его вдоль, то получится не два отдельных кольца, а одна целая лента.

Ориентированность

Данное свойство отсутствует у листа Мебиуса. Так как если бы кто-либо мог путешествовать по всем изгибам листа Мебиуса, то когда он вернулся бы в исходную точку, то превратился бы в свое зеркальное отражение.

Хроматический номер

"Хроматический номер" - максимальное число областей, которые можно нарисовать на поверхности так, чтобы каждая из них имела общую границу со всеми другими.

Хроматический номер

Если каждую такую область выкрасить по-разному, то любой цвет должен соседствовать с любым другим. Так вот, на листе бумаги, даже если его склеить в кольцо, еще никому не удалось расположить пять цветных пятен любой формы, которые имели бы всеобщую границу.

И на сфере, и на цилиндре их может быть не более четырех. Это и значит, что хроматический номер этих поверхностей – четыре. А на бублике число соответствующих цветов равняется семи. Каков же хроматический номер ленты Мебиуса? Он, как ни поразительно, равен шести.

На самом деле с листом Мебиуса возможно провести еще множество экспериментов и все они наверняка смогут удивить нас своими непредсказуемыми результатами.