Использование кругов Эйлера при построении урока информатики

В первый раз столкнувшись с понятие "круги Эйлера" многим может показаться, что они ничего о них не слышали и ничего не знают о применение данной методики на практике. На самом деле это нет так.

Совершая ежедневные мыслительные, логические процессы, мы подсознательно используем данные круги, но воспроизводим их в письменном, визуальном виде.

Круги Эйлера – это геометрическая схема, которая помогает находить и (или) делать наглядными логические связи между явлениями, процессами и понятиями. Также схема помогает изобразить отношения между каким-либо множеством и его частью

Круги могут делиться в зависимости от типа отношений между множествами, представляя всевозможные варианты использования для выделения логических взаимосвязей:

Круги Эйлера

• равнозначные (рис. 1)
• пересекающиеся (рис. 2)
• подчиненные (рис. 3)
• соподчиненные (рис. 4)
• противоречащие (рис. 5)
• противоположные (рис. 6)

Автор данного метода - ученый Леонард Эйлер (1707-1783). В одной из своих научных работ по теории числе учений сказал: "Круги подходят для того, чтобы облегчить наши размышления". Эйлер считается немецким, швейцарским и даже российским математиком, механиком и физиком. Дело в том, что он много лет проработал в Петербургской академии наук и внес существенный вклад в развитие в том числе и российской науки.

Метод Эйлера получил всеобщее внимание и заслуженное признание. Многие ученые использовали его в своей работе, в процессе доработки видоизменяли на свой лад. Так, чешский математик Бернард Больцано использовал тот же метод, но с прямоугольными схемами.

Свой вклад в дальнейшее использование метода кругов Эйлера внес немецкий математик Эрнест Шредер. Но основная заслуга принадлежат англичанину Джону Венну, специалисту по логике и автору книги "Символическая логика", где подробно было изложено его вариация применения метода (использование преимущественно изображения пересечений множеств). Благодаря работе Венна метод принято называть диаграммами Венна или Эйлера-Венна.

Использование кругов Эйлера можно встретить в различных сферах деятельности, но в своей статья я бы хотела рассмотреть их применение в образовательном процессе, а именно применить данную методику в построение уроков информатики. В наше время вокруг нас собрано огромное количество информации, и разобраться в ней бывает непросто.

Находить логические связи между явлениями и понятиями помогают "Круги Эйлера" – это практичный и удобный метод решения логических задач. Применение кругов Эйлера обеспечивает простоту, наглядность и быстроту решения задач не только информатики, но и иных предметных областях.

Практическое применение кругов Эйлера находит себя при решении определенного типа задач, например, используется в теории множеств как схематичное изображение всех возможных пересечений нескольких множеств. В общем случае они изображают все 2n комбинаций n свойств.

Например, при n=3 диаграмма Эйлера-Венна обычно изображается в виде трех кругов с центрами в вершинах равностороннего треугольника и одинаковым радиусом, приблизительно равным длине стороны треугольника.

В информатике с использованием кругов Эйлера можно решать задачи на построение запросов для поисковых систем или подсчитывать количество страниц по запросам. При изучении темы “Поиск информации в Интернет” рассматриваются примеры поисковых запросов с использованием логических связок.

Следует иметь ввиду, что в языке запросов поискового сервера для обозначения логической операции "ИЛИ" (объединение) используется символ "|", а для обозначения логической операции "И" (пересечение) – символ "&".

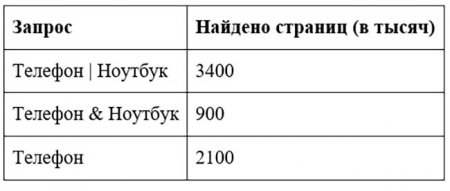
Приведем наглядный пример на задаче в формате ГИА и ЕГЭ по теме: "Поиск информации в Интернет": "В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет".

Запросы и количество найденных по ним страниц

Какое количество страниц (в тысячах) будет найдено по запросу Ноутбук?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Решение

Пусть:

Ф – количество страниц (в тысячах) по запросу Телефон;
Э – количество страниц (в тысячах) по запросу Ноутбук;
Х – количество страниц (в тысячах) по запросу, в котором упоминается Телефон и не упоминается Ноутбук;
У – количество страниц (в тысячах) по запросу, в котором упоминается Ноутбук и не упоминается Телефон.

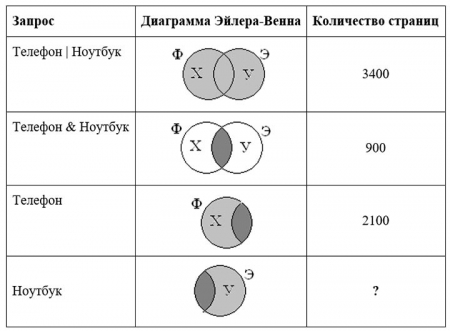
Построим диаграммы Эйлера для каждого запроса:

Диаграммы Эйлера для каждого запроса

Согласно диаграммам имеем:

1. Х+900+У = Ф+У = 2100+У = 3400. Отсюда находим У = 3400-2100 = 1300.

2. Э = 900+ У = 900+1300 = 2200.

Ответ: 2200.

Таким образом, круги Эйлера находят практическое применение при решении задач в формате ЕГЭ и ГИА и при решении содержательных логических задач. Круги Эйлера помогают быстро и просто решить даже достаточно сложные или просто запутанные на первый взгляд задачи.