Нетрадиционный способ решения задания № 18 ОГЭ по математике

Георг Александр Пик - австрийский математик, родившийся 10 августа 1859 года в еврейской семье. Георг Пик был одаренным ребенком, его обучал отец, который возглавлял частный институт.

Георг Александр Пик (1859-1942) - австрийский математик

В 16 лет Георг окончил школу, поступил в Венский университет, а уже в 20 лет получил право преподавать физику и математику.

В Немецком университете в Праге в 1888 году Пик получил место экстраординарного профессора математики, затем в 1892-м стал ординарным профессором. В 1900-1901 годах занимал пост декана философского факультета.

После того как Пик в 1927 году вышел в отставку, он получил звание почетного профессора и вернулся в Вену - город, в котором он родился. Однако в 1938 году он вернулся в Прагу.

За десять лет до того в 1928 году Пик был избран членом-корреспондентом Чешской академии наук и искусств, но в 1939-м, когда нацисты заняли Прагу, он был исключен из академии.

Теорема Пика не рассматривается в базовой школьной программе. Но, несомненно, она может облегчить решение задач на ОГЭ и ЕГЭ, в частности решение задания № 18 на экзамене в 9 классе по нахождению площади фигуры, представленной на клетчатой бумаге.

Теорема Пика помогает нам найти площадь фигуры, даже, без знания традиционных формул для нахождения ее площади.

Главное условие использования теоремы Пика – вершины многоугольника должны располагаться в узлах клеток.

Площадь фигуры на клетчатой бумаге можно вычислить, лишь, зная количество вершин у фигуры и количество узлов внутри нее. Чтобы вычислить площадь многоугольника по формуле Пика нужно:

1. Сосчитать количество целочисленных точек (узлов) внутри многоугольника (обозначается В);
2. Сосчитать количество целочисленных точек (узлов) на границе (вершин) многоугольника (обозначается Г);
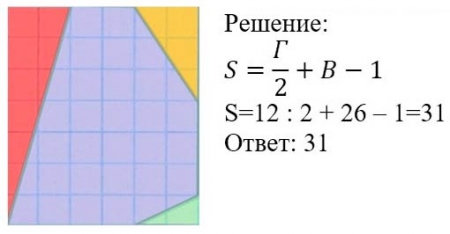
3. Применить формулу Пика Г : 2 + В – 1. Г : 2 + В – 1 , где В – количество узлов внутри многоугольника, а Г – количество вершин фигуры. (узлов на границе многоугольника)

Выполним сравнительный анализ нахождения площадей некоторых фигур на клетчатой бумаге. Конечно, если в задаче даны целочисленные значения, легче находить площадь квадрата, треугольника, параллелограмма, трапеции по традиционным формулам, нежели по формуле Пика.

Но, в случае, когда данные задачи не являются значениями целыми или даны более сложные фигуры, несомненно, проще применить формулу Пика:

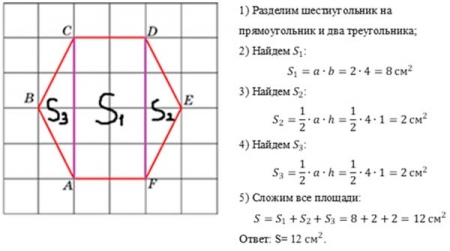
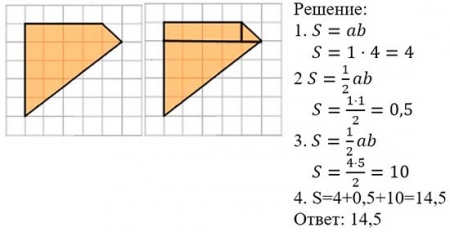
1. Найти площадь шестиугольника методом разбиения на части. Решение по традиционным формулам.

Найти площадь шестиугольника

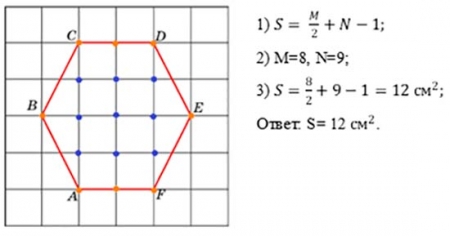
1.1 Найти площадь шестиугольника по формуле Пика

Найти площадь шестиугольника по формуле Пика

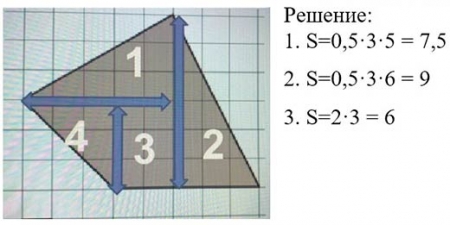
2. Найти площадь треугольника методом достраивания до прямоугольника.

Найти площадь треугольника

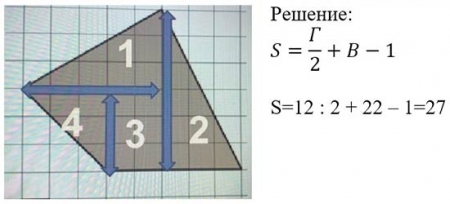
2.1 Найти площадь треугольника по формуле Пика.

Найти площадь треугольника по формуле Пика

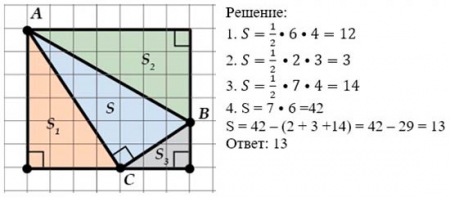
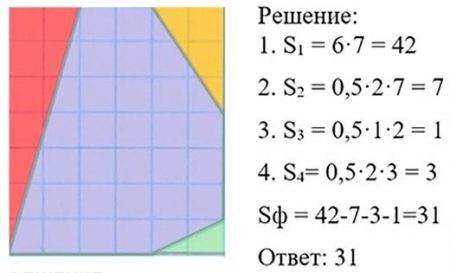
3. Найти площадь четырехугольника методом разбиения на части

Найти площадь четырехугольника методом разбиения на части

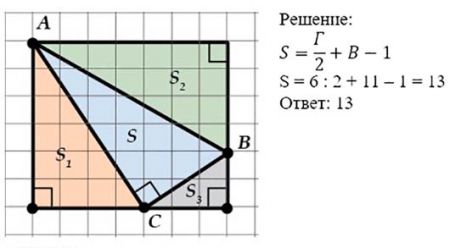
3.1 Найти площадь четырехугольника по формуле Пика.

Найти площадь четырехугольника по формуле Пика

4. Найти площадь четырехугольника методом разбиения на части.

Найти площадь четырехугольника

4.1 Найти площадь четырехугольника по формуле Пика.

Найти площадь четырехугольника по формуле Пика

5. Найти площадь шестиугольника методом достраивания до прямоугольника.

Найти площадь шестиугольника методом достраивания

5.1 Найти площадь шестиугольника по формуле Пика.

Найти площадь шестиугольника по формуле Пика

Формула Пика может применяться при решении заданий из ОГЭ на нахождение площади многоугольника, даже без клетчатой поверхности. Достаточно просто сделать клетчатую бумагу самим и подложить ее под фигуру, не забывая, что вершины многоугольника должны располагаться в узлах клеток.

Формула Пика - это настоящее спасение для тех учеников, которые так и не научились пользоваться традиционными формулами или для тех, кто так и не уяснил, как выполнить разбиение фигуры или дополнительное построение, чтобы воспользоваться формулами из справочного материала.