Конспект урока информатики 9 класс "Системы счисления"

Цели урока:

• познакомить учащихся 9 класса с общими представлениями о позиционных и непозиционных системах счисления;
• научить определять основание и алфавит системы счисления, переходить от свернутой формы записи числа к его развернутой записи.

Ход урока

Организационный момент

Для гармонизации двух полушарий предлагаю ребятам вначале медленно, а потом в более быстром темпе левой рукой взять правое ухо, а правой рукой взять левое ухо. Выполнять упражнение нужно несколько раз и в системе. Это снимает психологический стресс улучшает гармонизацию полушарий.

Постановка цели занятия

Эпиграф урока: "Все есть число и числа управляют миром".

- В качестве эпиграфа к сегодняшнему уроку я взяла два высказывания: первое – "Все есть число, и числа управляют миром". Так считали пифагорейцы, последователи философского учения Пифагора, античного ученого, известного вам из математики.

- А второе – высказывание академика А. Дородницына по поводу данного утверждения пифагорейцев: "Это, конечно, мистика. Но числа дают возможность человеку управлять миром, и в этом нас убеждает весь ход развития науки и техники".

Ответьте на вопрос: Почему оба высказывания актуальны и в настоящее время?
Обучающиеся: В настоящее время все большее значение приобретают информатизация общества и компьютеризация практически всех сфер деятельности человека.

Учитель: Правильно. А в каком виде представляется при этом информация, обрабатываемая и передаваемая с помощью компьютера? (в виде двоичного кода, т.е в виде последовательности нулей и единиц)

- Мы можем сказать, что информация – это числа, и эти числа действительно дают возможность человеку управлять различными процессами с помощью цифровой техники и науки информатики.

- Некоторые из вас готовили проект по определенной теме, остальные готовили опережающее задание. Подумайте и сформулируйте тему сегодняшнего урока. (формулируют тему урока)
- А сейчас давайте вместе с вами попытаемся сформулировать цели урока.

Обучающиеся: Сегодня на уроке мы рассмотрим такие понятия, как система счисления и цифры, определим разницу между позиционными и непозиционными системами счисления, узнаем, что такое основание позиционной системы счисления и ее алфавит.

Учитель: Правильно, а также рассмотрим машинные системы счисления и научимся выполнять перевод чисел из любой системы счисления в десятичную.

Изучение нового материала

- Современный человек каждый день запоминает номера машин и телефонов, в магазине подсчитывает стоимость покупки, ведет семейный бюджет и т.д. Числа, цифры… они с нами везде.
- Сколько цифр вам знакомо? (ответы обучающихся)
- А что такое число?

Цифры – это символы, участвующие в записи числа и составляющие некоторый алфавит. Число – некоторая величина

- Первоначально число было привязано к тем предметам, которые пересчитывались. Далее понятие числа развивалось в математике и сегодня считается фундаментальным понятием не только математики, но и информатики.

- Как вы думаете, почему люди разных стран говорят на разных языках, а считают одинаково?
- В первую очередь это связано с торговыми расчетами. Еще в древности при покупке и продаже разных товаров люди пришли к выводу, что считать и записывать количество товаров удобней одинаково, так как это значительно облегчает вычисления.

- А сейчас все попытайтесь решить вот такую задачу?

Задача

- Чтобы решить задачу, какие вопросы вы себе задавали? Что вам нужно знать?

Обучающиеся формулируют вопросы вслух: Например: "Почему вы называли так, а не как мы привыкли?", "Почему числа записаны только с помощью "0" и "1"?",
"В какой системе счисления записаны числа?", "Как записываются десятичные числа в двоичной системе счисления?", "Какие системы счисления бывают?", "Какие системы счисления используются в нашей жизни?" т.д.

- Числа складываются из цифр по определенным правилам. Известно множество способов представления чисел. В любом случае число изображается символом или группой символов. На разных этапах развития человечества, у разных народов эти правила были различны и сегодня мы их называем системами счисления.

- Кто может сказать, что такое система счисления? (Система счисления – это способ записи чисел с помощью цифр)
- Все известные системы счисления делятся на позиционные и непозиционные. И об этом мы послушаем проект, который нам подготовили обучающиеся.

- Сейчас, эта группа презентует свою работу, а все остальные слушают, анализируют, задают вопросы, можно также оставлять комментарии в письменном виде. (Идет защита деятельности группы)

Проект "Позиционные и непозиционные системы счисления"

- Прежде, чем решить задачу давайте с вами рассмотрим системы счисления, которые получили название "машинные", такие системы счисления, как двоичная, восьмеричная и шестнадцатеричная. Но, конечно, самой распространенной является десятичная позиционная система счисления.

- Любое число, записанное в позиционной системе счисления с произвольным основанием можно записать в виде полинома (многочлена). Приведем пример записи числа в десятичной системе счисления: 34510 = 3*102+4*101+5*100

- Необходимо запомнить, что количество цифр для записи числа в любой системе счисления не может превышать основания этой системы. Например, в двоичной системе счисления будет только две цифры: 0 и 1.

- Кто из вас попробует расписать эту систему счисления в виде многочлена? (вызывается обучающийся)
- А сколько цифр будет, например, в пятеричной системе счисления? (будет только пять цифр: 0, 1, 2, 3 и 4)
- А теперь давайте вместе с вами научимся переводить числа из двоичной системы счисления в десятичную.

- Итак, 1010102 = 1*25+0*24+1*23+0*22+1*21+0*20 = 32+8+2=42
- А теперь давайте вместе с вами научимся переводить числа из восьмеричной системы счисления в десятичную (вызывается обучающийся): 1238 = 1*82+2*81+3*80=64+16+3=83

- А теперь давайте вместе с вами научимся переводить числа из шестнадцатеричной системы счисления в десятичную.
- Для этого выясним для начала, каков алфавит этой системы счисления.

- Раз в десятичной системе счисления в записи чисел используется 10 цифр, в двоичной – 2, в восьмеричной – 8, то соответственно в шестнадцатеричной
– 16 цифр. Какие? (0, 1, … 9, А (10), В (11), С (12), D (13), E (14), F (15)
- Итак, 1А316 = 1*162+10*161+3*160 = 256+160+3 = 419

- Кроме привычной десятичной системы счисления существуют системы счисления с различными основаниями. Я просила вас подготовить небольшие сообщения о системах счисления, встречающихся в повседневной жизни.

Cообщения обучающихся

Двенадцатеричная система счисления: на ее широкое использование в прошлом явно указывают названия числительных во многих языках, а так же сохранившиеся в ряде стран способы отсчета времени, денег и соотношения между некоторыми единицами времени. Год состоит из 12 месяцев, а половина суток из 12 часов.

В русском языке счет часто идет дюжинами, чуть реже гроссами. О существовании 12ричной системы счисления говорит тот факт, что сервизы, салфетки, столовые приборы продают наборами по 6 или 12 штук.

Пятеричная система счисления.

Двадцатеричная система счисления.

Шестидесятеричная система счисления. Измерение времени и градусной меры углов основывается на шестидесятеричной системе счисления древних шумеров. В Древнем Вавилоне использовалась система счисления с основанием 60. Делением часа на 60 минут, а минут на 60 секунд мы обязаны этой системе счисления.

- Система гадания китайской "Книги перемен" ("И-Цзин"), уходящая корнями в глубокую древность, при внимательном анализе обнаруживает в своей основе двоичную систему счисления и позиционный принцип записи числа.

- Двоичная система мер используется в ЭВМ. Кроме приведенных систем счисления следует отметить и более экзотические, такие как одиннадцатеричная система счисления на островах Океании.

Дифференцированная самостоятельная работа

Для закрепления и проверки знаний проводится дифференцированная самостоятельная работа.
- Итак, мы с вами рассмотрели позиционные и непозиционные системы счисления. А сейчас выполните самостоятельную работу. Каждый из вас выберет задание, с которым он может справиться.

- Те, кто закончит раньше остальных, положите ручки на парту и отдохните под музыку. (Муз. пауза)
- А перед тем как приступить к выполнению самостоятельной работы, проведем физкультминутку.

Мозговая гимнастика

Качания головой

Упражнение стимулирует мыслительные процессы. Дышите глубоко, расслабьте плечи и уроните голову вперед. Позвольте голове медленно качаться из стороны в сторону, пока при помощи дыхания уходит напряжение. Подбородок вычерчивает слегка изогнутую линию на груди по мере расслабления шеи. Выполнять 30 секунд.

"Ленивые восьмерки"

Упражнение активизирует структуры мозга, обеспечивающие запоминание, повышает устойчивость внимания.
Нарисовать в воздухе в горизонтальной плоскости "восьмерки" по три раза каждой рукой, а затем обеими руками.

Самостоятельная работа на тему "Системы счисления" (на оценку "3")

1. Верно ли, что в каменном веке считали в двоичной системе счисления?
2. Верно ли, что в Древнем Вавилоне цифры изображались с помощью иероглифов?
3. Верно ли, что на Руси не было специальных обозначений для цифр, а пользовались буквами с "титлом"?
4. Верно ли, что в Древнем Риме нельзя было делить числа "в столбик"?
5. Верно ли, что число 34263 может быть записано в пятеричной системе счисления?
6. Верно ли, что в древности использовали руку, как инструмент для счета?
7. Верно ли, что число 1001101 может быть записано в двоичной системе счисления?
8. Верно ли, что арабские цифры изобрели арабы?
9. Верно ли, что клинописью пользовались в Древнем Египте?
10. Верно ли, что римская система счисления была непозиционной?

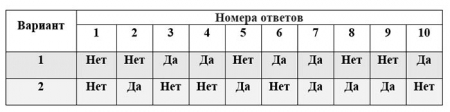
Таблица для проверки результатов

Ответы к тесту на оценку "3"

На оценку "4"

1. Система счисления – это:

а) представление чисел в экспоненциальной форме;
б) способ представления чисел с помощью заданного набора специальных знаков (цифр);
в) способ представления десятичных чисел;
г) способ представления двоичных чисел.

2. Какие числа используются для представления чисел в пятеричной системе счисления?
а) 1, 2, 3, 4, 5;
б) 0, 1, 2, 3, 4, 5;
в) 0, 1, 2, 3, 4;
г) 0, 5

3. Сколько раз встречается цифра 2 в записи первых 10 чисел (начиная с 1) в системе счисления с основанием 4?
а) 2;
б) 3;
в) 4;
г) 6

4. Килограмм конфет "Косолапый мишка" стоит 5710 руб, а килограмм конфет "Красная шапочка" 1110102 руб. Какие конфеты дороже?

Ответы: 1.б, 2.в, 3.г, 4. Красная шапочка

На оценку "5"

Перевести в десятичную систему счисления: 101102 (22) , 7518 (489), 22С16 (556), 1А916 (425)

Учитель: Скажите, пожалуйста, сейчас мы сможем решить задачу, заданную в начале урока и ответить на вопросы?
Ответ: братьев – 3, старшему брату – 16, учится старший брат в 10 классе. Мы находимся в двоичной системе счисления.

Подведение итога урока

- Проверим, насколько внимательны вы были сегодня на уроке – ответьте на следующие вопросы:

• Какие народности использовали непозиционные системы счисления? (Древние египтяне, греки, римляне)
• Основание Вавилонской системы счисления. (60)
• Где зародилась десятичная система счисления? (в Индии)

- Вы сегодня работали хорошо, справились с поставленной перед вами задачей, а также показали хорошие знания по теме "Системы счисления".
- За работу на уроке вы получаете следующие оценки. (объявляются оценки каждого обучающегося за работу на уроке)
- Спасибо всем за хорошую работу. Молодцы!

Домашнее задание

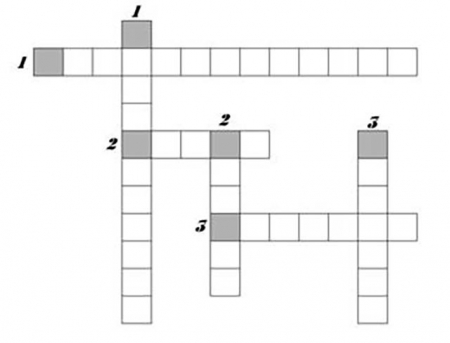
Кроссворд "Системы счисления. Основные понятия"

Кроссворд "Системы счисления"

По горизонтали:

1. Система, в которой количественное значение цифры не зависит от ее положения в числе. (непозиционная)
2. Символы, при помощи которых записывается число. (цифра)
3. Самый яркий пример непозиционной системы счисления. (римская)

По вертикали:

1. Система, в которой количественное значение цифры зависит от ее положения в числе. (позиционная)
2. Как называется позиция цифры в числе. (разряд)
3. Совокупность различных цифр, используемых а позиционной системе счисления для записи чисел. (алфавит)

sistemy-schisleniya.rar

Размер:

124.88 Kb

Скачали:

10