Сборник практико-ориентированных задач по математике для 5-9 классов

Главная » Средние классы » Разное

В сборник практико-ориентированных задач по математике для учащихся 5-9 классов вошли задачи из следующих разделов:

Задачи с экологическим содержанием (5-6 класс)
Задачи на растворы и сплавы (6-7 класс)
Задачи на выполнение плановых заданий (7 класс)

Задачи на изменение количества
Задачи на сплавы и смеси
Площадь прямоугольника
Задачи на движение
Задачи на движение по реке
Алгебраические дроби (8 класс)
Квадратные корни

Сборник задач по математике

Задачи с экологическим содержанием (5-6 класс)

Задача № 1
Один гектар леса в течение года способен поглощать столько углекислого газа, сколько его выделяют 232 человека. Сколько процентов это составляет от общего числа людей, проживающих в Кировской области. (в 2014 году численность составила 487 136 человек)

Сколько гектаров леса должно находиться в пределах города, чтобы в чистоте содержать воздух города?

Ответ: примерно 0,05%; 2100 га.

Задача № 2
Вырубая один гектар леса, наносят огромный урон составу воздуха. Ведь за один солнечный день 1 га леса поглощает из воздуха до 280 кг углекислого газа и выделяет до 200 кг кислорода. Также 1 га лиственного леса за год задерживает до 100 тонн пыли, хвойного – до 40 тонн.

Задание 1. Сколько кг углекислого газа поглощается в солнечные дни лесом в Кировской области в год, если считать, что солнечных дней в году примерно 97, а площадь лесов составляет 8,14 млн. га?

Задание 2. На сколько процентов больше поглощается углекислого газа, чем выделяется кислорода?

Задание 3. Сколько тонн пыли за полгода задерживают 4055,1 тыс. га хвойных и 3519,8 тыс. га лиственных лесов Кировской области?

Задача № 3

Объемы выполняемых лесовосстановительных работ в Кировской области обеспечивают своевременное восстановление лесов на вырубаемых площадях и сокращение непокрытых лесной растительностью земель лесного фонда.

В 2016 году мероприятия по воспроизводству лесов выполнены на площади 35012 га при годовом плане 26699 га. На сколько процентов перевыполнен план по воспроизводству лесов?

Ответ: на 31%

Задача № 4
За 2016 год в рамках осуществления федерального государственного лесного надзора (лесной охраны) лесного фонда Кировской области было выявлено 6910 нарушений лесного законодательства, в том числе 303 случаев незаконных рубок лесных насаждений. Объем незаконно заготовленной древесины составил 17,0 тыс. куб. м.

Задание 1. Сколько % составляют случаи незаконной вырубки лесных насаждений от общего числа выявленных нарушений? Ответ: 4,4%

Задание 2. Вычислите стоимость ущерба от незаконно заготовленной древесины, если стоимость 1 куб.м составляет примерно 8, 2 тыс. руб.?

Задача № 5
Раскрываемость незаконных рубок леса в Кировской области в 2016 г. составляет 56,4% от общего количества случаев. В течение года возбуждено 169 уголовных дел по ст. 260 УК РФ. Найдите общее количество нарушений.

Задачи на растворы и сплавы (6-7 класс)

Задача № 1
Для приготовления блюда требуется на 50 г воды добавить 100 г 6%-го уксуса. У хозяйки имеется только 12%-й уксус. Сколько граммов 12%-го уксуса ей нужно добавить на 50 г воды, чтобы получить раствор нужной концентрации?

Ответ: 25 г.

Задача № 2
Сколько граммов воды нужно добавить к 180 г сиропа, содержащего 25% сахара, чтобы получить сироп, концентрация которого равна 20% ?

Ответ: 45 г.

Задача № 3
Два спиртовых раствора борной кислоты одинаковой массы слили в один сосуд. Раствор какой концентрации получили в результате, если первый раствор был 5%-ный, а второй 1%-ный?

Задача № 4

Сплавили 40 г золота одной пробы и 60 г золота другой пробы и получили золото 62 пробы. Какой пробы было золото первого и второго слитков, если при сплаве их поровну получается золото 61 пробы? (Проба – это процентное содержание чистого золота)

Ответ: 56 пробы и 66 пробы.

Задача № 5
Имеется два сплава с разным содержанием меди: в первом содержится 70%, а во втором - 40% меди. В каком отношении надо взять первый и второй сплавы, чтобы получить из них новый сплав, содержащий 50% меди?

Ответ: 1:2.

Задачи на выполнение плановых заданий (7 класс)

Задача № 1

Колхоз планировал провести сев за 14 дней. Перевыполняя план, колхозники засевали в день на 30 га больше, чем планировалось, и уже за 4 дня до срока им оставалось засеять 20 га. Сколько гектаров должен засеять колхоз?

Обозначив буквой х дневную норму сева (в га), выразите:

а) сколько всего гектаров должен засеять колхоз;
б) сколько гектаров засевалось за 1 день;
в) сколько гектаров было засеяно за 4 дня до срока.

Сравните число засеянных за 4 дня до срока гектаров с числом гектаров, которые планировал засеять колхоз за 14 дней, и напишите уравнение. Решите уравнение и запишите ответ на вопрос задачи.

Дополнительные вопросы:

На сколько процентов колхозники перевыполнили дневную норму? (Ответ округлите до десятых долей процента)
На сколько процентов был выполнен план посева за 4 дня до срока?

Задача № 2
На строительстве плотины ГЭС укладчики бетона, перевыполняя дневную норму на 180 м³, не только выполнили 10-дневное задание за один день до срока, но и уложили дополнительно 320 м3 бетона. Какова была дневная норма укладки бетона?

Задача № 3
Чтобы выполнить задание в срок, токарь должен изготавливать за каждый рабочий день 24 детали. Однако, применив новый тип резца, он изготавливал за рабочий день на 15 деталей больше, и уже за 6 дней до срока изготовил сверх плана 21 деталь. Сколько всего деталей изготовил слесарь?

Задачи на изменение количества

Задача № 1
Один фермер заготовил в 1,5 раза больше сена, чем второй. Ежедневно первый расходовал по 0,5 т сена, а второй по 0,3 т. Через 70 дней у первого фермера осталось на 12 т сена больше, чем у второго. Сколько сена заготовил каждый фермер?

Обозначив буквой х количество сена, заготовленного вторым фермером, выразите:

а) сколько тонн сена заготовил первый фермер;
б) сколько тонн сена израсходовал каждый фермер за 70 дней;
в) сколько тонн сена осталось у каждого фермера через 70 дней.

Сравните количества сена, оставшегося у фермеров, и запишите уравнение. Решите уравнение и запишите ответ на вопрос задачи.

Дополнительные вопросы:

На сколько процентов больше сена окажется у первого фермера, чем у второго, через 70 дней?
У кого из фермеров раньше иссякнет запас сена, если расход сена будет тем же?

Задача № 2
В одном овощехранилище было 440 т картофеля, а в другом – 408 т. Из первого хранилища ежедневно вывозили по 60 т, а во второе ежедневно завозили по 48 т картофеля. Через сколько дней во втором овощехранилище окажется в три раза больше картофеля, чем в первом?

Задача № 3
В одном баке – 940 л воды, а в другом – 480 л. Из первого выливают за час в 3 раза больше воды, чем из второго. Через 5 ч в первом баке останется на 40 л меньше воды, чем во втором. Сколько литров воды выливается из каждого бака за 1 час?

Задачи на сплавы и смеси

Задача № 1
Сплав меди и цинка содержит 82% меди. После добавления в сплав 18 кг цинка процентное содержание меди в сплаве понизился до 70%. Сколько меди и сколько цинка было в сплаве первоначально?

Обозначив буквой х первоначальную массу сплава в килограммах, выразите:

а) Массу меди в сплаве;
б) массу сплава после добавления цинка;
в) отношение массы меди к новой массе сплава.

Составьте уравнение, учитывая, что процент содержания мадии в полученном сплаве известен. Решите уравнение и найдите массы меди и цинка в первоначальном сплаве.

Дополнительные вопросы:

Сколько цинка нужно было добавить в первоначальный сплав, чтобы его процентное содержание составило 50%?
Можно ли, добавляя в первоначальный сплав равные массы меди и цинка, получить сплав, содержащий 50% цинка?

Задача № 2
Сплав олова и меди, масса которого 16 кг, содержит 55% олова. Сколько килограммов олова нужно добавить, чтобы повысить содержание олова в сплаве до 60%?

Задача № 3
К 27 кг сплава и олова, содержащего 40% свинца, добавили некоторое количество свинца, в результате чего содержание олова в сплаве понизилось на 6%. Сколько килограммов свинца было добавлено в сплав?

Площадь прямоугольника

Задача № 1
Длина прямоугольника на 18 м больше его ширины. Если длину прямоугольника уменьшить на 7 м, то его площадь увеличится на 40 м2. Найдите площадь прямоугольника.

Обозначив буквой х ширину прямоугольника в метрах, выразите:
а) длину прямоугольника в метрах;
б) площадь прямоугольника в квадратных метрах;
в) длину и ширину прямоугольника после изменения его измерений;
г) площадь измененного прямоугольника в квадратных метрах.

Сравните площади данного и измененного прямоугольника и запишите уравнение. Решите уравнение и запишите ответ на вопрос задачи.

Дополнительные вопросы:

Какой из прямоугольников, данный или измененный, имеет больший периметр?
На сколько процентов площадь данного прямоугольника меньше площади измененного прямоугольника?

Задача № 2
Длина прямоугольника в два раза больше его ширины. Если ширину прямоугольника увеличить на 8 дм, а длину уменьшить на 10 дм, то площадь прямоугольника увеличится на 220 дм². Найдите площадь данного прямоугольника.

Задача № 3
Периметр прямоугольника равен 60 см. Если длину прямоугольника увеличить на 10 см, а ширину уменьшить на 6 см, то площадь прямоугольника уменьшится на 32 см². Найдите площадь данного прямоугольника.

Задачи на движение

Задача № 1
Из пункта M в пункт N велосипедист ехал по шоссе со скоростью 16 км/ч, а возвращался по проселочной дороге, которая была на 6 км длиннее. Сколько километров проехал велосипедист по шоссе и сколько по проселочной дороге, если на весь путь он затратил 4 ч?

Обозначив буквой x длину пути по шоссе (в километрах), выразите:

а) длину пути велосипедиста по проселочной дороге;
б) время (в часах), затраченное велосипедистом на путь по шоссе;
в) время (в часах), затраченное велосипедистом на путь по проселочной дороге.

Учитывая, что время, затраченное на весь путь, известно, составьте уравнение. Решите уравнение и запишите ответ.

Дополнительные вопросы:

Какова средняя скорость велосипедиста на всем маршруте?
Сколько времени затратил бы велосипедист на весь путь, если бы по проселочной дороге он ехал на 3 км/ч быстрее, а по шоссе на 4 км/ч медленнее?

Задача № 2
Лыжная трасса состоит из подъема и спуска, причем подъем на 8 км короче спуска. Лыжник, двигаясь на спуске со скоростью 18 км/ч, а на подъеме со скоростью 8 км/ч, затратил на подъем на 15 мин больше, чем на спуск. Найдите длину каждого участка трассы.

Обозначив буквой х длину спуска (в километрах), выразите:

а) длину подъема в километрах;
б) время (в часах), затраченное на спуск;
в) время (в часах), затраченное на подъем.

Сравнив время, затраченное на спуск и подъем, составьте уравнение. Решите уравнение и запишите ответ.

Дополнительные вопросы:

Какова средняя скорость лыжника на всей трассе?
Сколько времени затратит лыжник на обратный путь, если будет двигаться на подъеме со скоростью 8 км/ч, а на спуске 18 км/ч?

Задача № 3
Из пункта А в пункт В со скоростью 66 км/ч отправился товарный поезд, а спустя 20 мин из пункта В в направлении пункта А вышел скорый поезд, проходящий в час 90 км. На каком расстоянии от пункта А встретятся поезда, если длина перегона АВ равна 256 км?

Обозначив, буквой х время движения (в часах) товарного поезда до встречи со скорым, выразите:

а) время движения скорого поезда;
б) путь, пройденный товарным поездом до встречи со скорым;
в) путь, пройденный скорым поездом до встречи с товарным.

Учитывая, что суммой путей, пройденных обоими поездами до их встречи, равна АВ, составьте уравнение. Решите уравнение и запишите ответ.

Дополнительные вопросы:

Какой из поездов прошел до встречи больший путь?
Какой из поездов прибыл раньше: товарный в пункт В или скорый в пункт А?

Задачи на движение по реке

Задача № 1
Лодка проплыла по течению реки на 11 км больше, чем против течения, затратив на весь путь 3 часа. Зная, что скорость лодки в стоячей воде равна 5 км/ч, а скорость течения 2 км/ч, определите, сколько всего километров проплыла лодка.

Обозначив, буквой х расстояние (в километрах), пройденное лодкой против течения реки, выразите:

а) расстояние (в километрах), пройденное лодкой по течению реки;
б) скорость лодки по течению и против течения реки;
в) время движения лодки по течению и против течения реки.

Учитывая, что на весь путь лодка затратила 3 ч, составьте уравнение. Решите уравнение и запишите ответ.

Дополнительные вопросы:

Какова средняя скорость движения лодки на всем пути?
Сколько времени потребовалось лодке, чтобы проплыть то же расстояние в стоячей воде?

Задача № 2
Моторная лодка прошла по реке 46 км за 3 часа, причем часть пути против течения, а часть по течению реки. Зная, что скорость течения реки 1 км/ч, а скорость лодки в стоячей воде 15 км/ч, определите, сколько километров прошла лодка по течению и сколько против течения реки.

Обозначив, буквой х путь (в километрах), пройденный лодкой против течения реки, выразите:

а) путь, пройденный по течению реки;
б) скорость лодки по течению и против течения реки;
в) время движения лодки по течению и против течения реки.

Дополнительные вопросы:

Какова средняя скорость движения лодки на всем пути?
Сколько времени потребовалось лодке, чтобы проплыть то же расстояние в стоячей воде?

Алгебраические дроби (8 класс)

Задача № 1
Ученик, отработав в школьной трудовой бригаде две недели, получил заработную плату, и решил положить ее на счет в банке. Он может открыть счет с годовым доходом 8%. Если бы банк выплачивал 11% годовых, то для получения такого же дохода потребовалось бы на 900 рублей меньше. Определите, сколько рублей составила заработная плата.

Ответ: 3300р.

Задача № 2
Два ученика вместе могут набрать текст на компьютере за 2 ч. Первому ученику на эту работу потребовалось бы на 3 ч больше, чем второму. За какое время может набрать текст на компьютере первый ученик?

Ответ: за 6 часов

Задача № 3
Путь от Кыштыма до Екатеринбурга автомобиль проезжает за 2.5 часа. Если он увеличит скорость на 20 км/ч, то за 2 ч он проедет путь на 15 км больший, чем расстояние от Кыштыма до Екатеринбурга. Найдите это расстояние.

Ответ: 125 км

Задача № 4.
Татьяна прошла от дома до школы и вернулась обратно, затратив на весь путь 1 час. О дома до школы она шла со скоростью 4 км/ч, а на обратном пути ее скорость была 6 км/ч. Чему равно расстояние от дома Тани до школы.

Ответ: 2,4 км

Задача № 5
Расстояние между г. Кыштымом и г. Касли равно 30 км. Из г. Кыштыма в направлении г. Касли выехал мотоциклист со скоростью 40 км/ч. Одновременно из города Касли в ом же направлении выехал велосипедист со скоростью 10 км/ч. На каком расстоянии от г. Касли мотоциклист догонит велосипедиста.

Ответ: 10 км.

Квадратные корни

Задача № 1
Стебель камыша выступает из воды озера на 1 м. Его верхний конец отклонили от вертикального положения на 2 м, и он оказался на уровне воды. Найдите глубину озера в месте, где растет камыш.

Камыш выступает из воды озера на 1 м

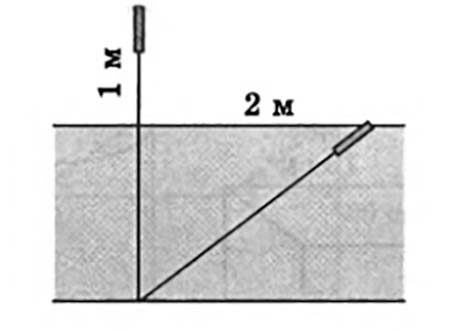
Задача № 2
В 60 метрах одна от другой растут две сосны. Высота одной 31 м, а другой – 6 м. Найдите расстояние между их вершинами.

Расстояние между соснами

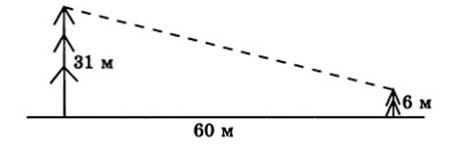
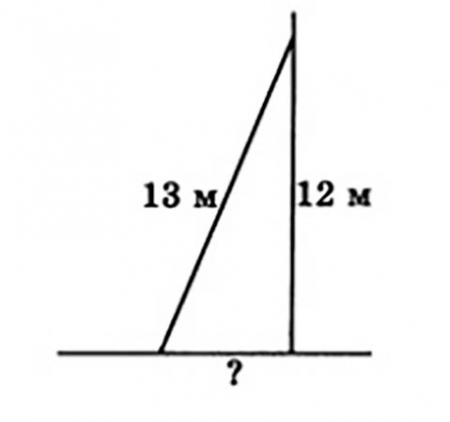
Задача № 3
На какое расстояние следует отодвинуть от стены дома нижний конец лестницы, длина которой 13 м, чтобы верхний ее конец оказался на высоте 12 м?

Лестница у стены дома

Задача № 4
Мальчик прошел от дома по направлению на восток 800 м. Затем повернул на север и прошел 600 м. На каком расстоянии от дома оказался мальчик?

Путь, который прошел мальчик

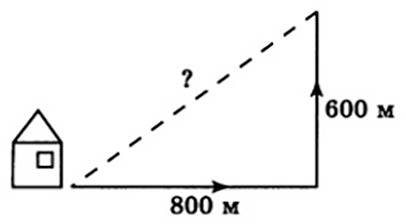
Задача № 5
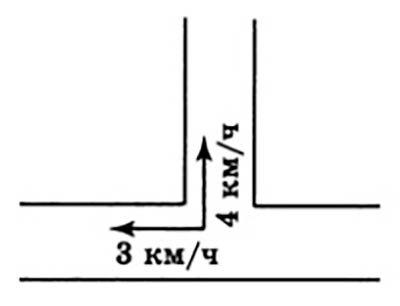
Сергей и Таня, расставаясь на перекрестке, пошли по взаимно перпендикулярным дорогам, мальчик со скоростью 4 км/ч, девочка – 3 км/ч. Какое расстояние (в км) будет между ними через 30 мин?

Скорость движения мальчика и девочки