Элементы логики на уроках математики

Количество информации, окружающее человека в современном мире выросло в разы за последнее время. А огромные возможности ее получения создают такие условия, что не обязательно думать, достаточно нажать кнопку гаджета, пролистать страницы, рисунки, схемы.

А сам мыслительный процесс, как следствие, превращается в тяжелый труд.

Все чаще от школьника слышно, что трудно решить задачу, содержащую 2–3 шага рассуждений. Обучающиеся плохо говорят, кто-то и двух слов не может связать, кто-то говорит несвязно, перечисляя все факты подряд, которые разобрать невозможно. Проблема возникает и на точных предметах, и на гуманитарных.

Умение решать геометрические задачи части с развернутыми ответами, особенно на доказательство, на выпускных экзаменах (ОГЭ, ЕГЭ) достигает менее 10%. Основная причина – нарушение логики решения. Обучающиеся не могут объяснить свои выводы.

Все реже школьники могут отстоять свою точку зрения, проанализировать создавшуюся ситуацию и оценить риски последствия своих действий. Таким образом, знакомство с законами логики становится на сегодняшний день очень актуальным.

Знакомясь на уроках информатики с некоторыми логическими элементами, обучающиеся не всегда могут их перенести на другие предметы, необходимы иллюстрации их применения и в разделах математики и в повседневной речи. В разные периоды развития школьного образования нашей страны логика была обязательным предметом. А именно, в дореволюционной России, в послевоенный период (до 1956 года).

В настоящее время этот раздел практически не отражен в учебной литературе. Элементы логики вводятся в курс вероятности и статистики, но информации по-прежнему мало.

А ведь именно логика приучает точно мыслить, формирует ясную речь, привычку анализировать свои и чужие рассуждения, учит спорить и опровергать ошибочные рассуждения, вырабатывает привычку думать. И, безусловно, логика оказывает неоспоримую помощь в переводе мыслительного процесса из разряда тяжелого труда в разряд привычки, доставляющей наслаждение.

Учитель математики имеет возможность ненавязчиво, но систематические знакомить обучающихся на своих уроках с основными законами логики, обращая внимание на значимость всем известных связок "и", "или", "если…, то…".

Обучая умению строить отрицания, искать противоречия, развивать критическое мышление, практически на каждом уроке алгебры, геометрии или вероятности и статистики можно обращать внимание учеников на то, что правильность рассуждений основывается на грамотном использовании законов логики.

Рассмотрим примеры знакомства обучающихся с логическими рассуждениями на уроках алгебры и геометрии 7 класса. Начнем с определения истинности высказываний, предложений, о которых можно однозначно сказать, истинны они или ложны. На вопрос верно/неверно ученики отвечают охотно.

Задание такого рода содержится в КИМ ГИА 9 в разделе геометрии и КИМ ГИА 11 базового уровня. На занятиях полезно сопоставлять высказывания, описывающие обычные жизненные ситуации с математическими утверждениями, показывая применение законов логики для их обоснований.

Важнейшими логическими связками являются "и" и "или". Отработка их понимания способствует большему пониманию математических рассуждений и совершенствованию умений вести беседы, аргументированные споры. Например:

Следует обратить внимание обучающихся на то, что слово "или" и в обычной речи, и в математике имеет два значения – разделительное и неразделительное. Во многих случаях, какое значение имеет фраза, легко понять по ее смыслу. А ввиду того, что разделительное "или" можно считать частным случаем неразделительного, за основу принимается неразделительное. В математике говорим о строгой и нестрогой дизъюнкции.

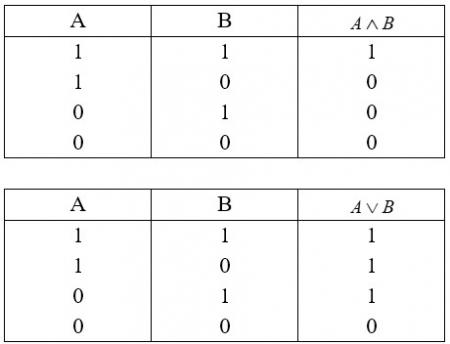
Анализируя высказывания, необходимо рассуждать об их истинности или ложности. Полезно с обучающимися составить таблицы истинности для высказываний со связками "и", "или" (неразделительное). В логике такие высказывания называются соответственно конъюнкция и дизъюнкция:

Конъюнкция и дизъюнкция

Задания для обсуждения
Оля гуляла с Басей во дворе, спустив его с поводка, и оставив в наморднике. Прохожий упрекнул ее в нарушении правил содержания собак в городе. Листок с правилами был наклеен на информационном стенде и одно из них гласило: пес не должен перемещаться без намордника … поводка в местах скопления людей (кусочек бумаги после слов "без намордника" был оторван).

Оля возмутилась: "Разве это справедливо? Я действительно спустила Басю с поводка, но он же в наморднике! Кто же из нас прав?"
Вася решал неравенство |x|>5 и получил неравенства x>5, x<-5. В ответ записал: ∅. Вася считает, что нет таких чисел, которые больше 5 и меньше -5. В чем его ошибка?

Переформулируйте высказывание с помощью союза "или": "По крайней мере одно из чисел n, n + 1, n + 2 четно" Определите, истинно это утверждение или ложно.
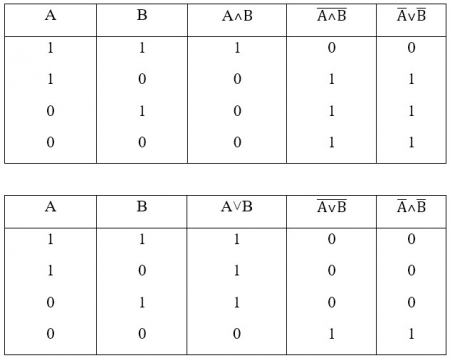
Частой проблемой для обучающихся является неумение построить отрицание высказываний.

Уже в начале изучения курса алгебры часто приходится отвечать на вопрос при каких значениях переменной произведение выражений равно нулю ил не равно нулю. Не всегда оказывается очевидным, что (2х+6)(2х-18)=0 при х=-3 ИЛИ х=9, (2х+6)(2х-18)≠0, если х≠-3 И х≠9. Обсудите на уроке утверждения: "Я попросил маму купить шоколадку ИЛИ мороженое".

"Я обещал другу решить первую И вторую задачи домашней работы". Как будут сформулированы утверждения, иллюстрирующие невыполнение (отрицание) приведенных просьб и обещаний? "Мама не купила ни шоколадку, ни мороженое". "Друг обиделся на меня, я решил только вторую задачу".

Таблицы истинности

Не все обучающиеся правильно понимают и используют предложения со словами все, каждый и не все, некоторые; по крайней мере, не более чем и т.п. А построение отрицания вызывает еще больше проблем. Что значит, неверно, что "все простые числа нечетные" или, например, "все ученики нашего класса – отличники".

Оказывается, если в простом предложении нет слов все, каждый или есть, некоторые, то для построения отрицания достаточно поставить перед сказуемым "не". Например: "Сегодня идет дождь", "число 4 – является четным". Их отрицания: "сегодня не идет дождь", "число 4 – не является четным".

Если же такие слова как все, любой, некоторый присутствуют в предложении, то при построении отрицания используется замена слов: все, любой, каждый ↔ существуют, некоторый, есть. Например, "в каждом городе есть метро".

Отрицание: "есть города, в которых нет метро". Что значит, неверно, что "все треугольники равнобедренные"? При отрицании: "существуют треугольники, которые не являются равнобедренными", или, " есть треугольники неравнобедренные". При построении новых высказываний необходимо анализировать их истинность.

Задания для обсуждения
Является ли отрицанием предложения "он – мой друг" предложение "он - мой враг"?

Сформулируйте отрицание для высказываний:
а) "Все французы живут во Франции";
б) "Найдется ромб, у которого соседние стороны не равны";
в) "При бросании симметричной монеты трижды, орел не выпал ни разу".

Объясните, что означает фраза "неверно, что Оля получила по алгебре по крайней мере одну двойку".

В любых рассуждениях из нескольких утверждений следуют определенные выводы. Без связки "если..., то…" нет обоснованных суждений, а в геометрии мы проводим доказательства утверждений на каждом шагу. Часто должны убеждаться в справедливости прямых и обратных рассуждений.

А одним из основных приемов доказательства многих теорем является доказательство от противного. По-прежнему нематематические утверждения облегчают понимание логики. Например, будем считать верным утверждение "если кот мяукает, то он хочет молока".

Какие из приведенных рассуждений следуют из этого утверждения:

1. если кот хочет молока, то он мяукает;
2. если кот не хочет молока, то он не мяукает;
3. кот или не мяукает, или хочет молока;
4. кот или мяукает, или не хочет молока.

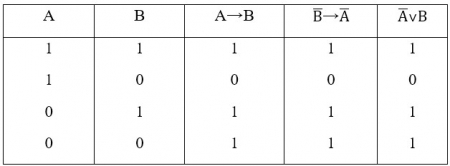
В обсуждении отмечаем, что 1-е и 4-е не следует из данного, а 2-е и 4-е следует. Причем, 2-е утверждение иллюстрирует справедливость применения метода от противного в доказательствах. Связка "если..., то…" в логике называется импликация. Составим таблицу истинности для импликации и добавим истинность утверждений 2 и 4 из приведенного примера:

Таблица истинности для импликации

Составив таблицу истинности, заметим, что для истинности высказывания "если…, то…" достаточно ложности посылки (А). Получаем, что справедлива нелепица, вроде "если 2 + 2 = 5, то Париж – столица Франции".

Значит, в логике использование связки "если…, то…" отличается от применения в обыденной речи, в которой мы подразумеваем, что В вытекает из А. То есть в речи между посылкой и заключением имеется причинно-следственная связь, а в логике этого не требуется. Но это уже более глубокое изучение проблемы.

Задания для обсуждения (ЕГЭ, математика, база)

Когда какая-нибудь кошка идет по забору, собака Жучка, живущая в будке возле дома, обязательно лает. Выберите утверждения, которые верны при приведенном условии.

1. Если Жучка не лает, значит, по забору идет кошка.
2. Если Жучка молчит, значит, кошка по забору не идет.
3. Если по забору идет сиамская кошка, Жучка не лает.
4. Если по забору пойдет кошка Муся, Жучка будет лаять.

В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
У А спрашивают: "Вы рыцарь?" Тот отвечает: "Если я рыцарь, то съем собственную шляпу". Докажите, что А придется съесть свою шляпу.

А утверждает: "Если я рыцарь, то дважды два – четыре". Кто такой А: рыцарь или лжец?
А заявляет: "Если я рыцарь, то дважды два – пять". Кто, по-вашему, А: рыцарь или лжец?

Известно, что х натуральное число. Даны три высказывания: А "Число х делится на 3", В "Число х делится на 6" и С "Число х четно". Какие их следующих высказываний истинны при любых значениях х?
А→В;
В→А;
В→С;
А→С?

Научить логически мыслить – одно из главных назначений обучения. Уметь устанавливать истинность рассуждений – непростая, но достижимая задача, решение которой требует ежедневного кропотливого труда.

Математика, как никакой другой предмет позволяет подготовить обучающихся к умению критически мыслить и обоснованно отстаивать свои убеждения. Систематическая работа над грамотностью повседневной речи, соотнесение высказываний с математическими утверждениями повысит интерес обучающихся к предмету.

И как будет приятно узнать Вашим обучающимся, что они научились говорить и мыслить по законам логики.