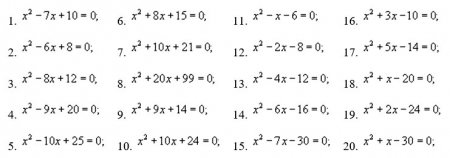Практическая работа по алгебре на тему "Линейные и квадратные уравнения и системы уравнений"

Главная » СПО, ВУЗ

Раздел: уравнения и неравенства.

Учебная цель:

восполнить некоторые содержательные пробелы основного курса;
создать в совокупности с основными разделами курса базу для развития способностей обучающихся, помочь осознать степень своего интереса к предмету.

Учебные задачи:

сформировать понятия: квадратное уравнение, приведенное квадратное уравнение, полное квадратное уравнение, неполное квадратное уравнение;
научить различать виды неполных квадратных уравнений и решать эти уравнения;
развивать навыки творческой, познавательной, мыслительной деятельности, логическое мышление;
развивать интерес к математике, самостоятельность, прививать аккуратность и трудолюбие.

Образовательные результаты, заявленные в ФГОС:

Студент должен

уметь:

решать линейные и квадратные уравнения;
распознавать квадратные уравнения, приводить примеры;
распознавать неполные квадратные уравнения, приводить примеры, решать данные уравнения;
находить дискриминант;
определять число корней квадратного уравнения в зависимости от дискриминанта;
находить корни квадратного уравнения по формуле;
составлять квадратное уравнение по известным корням;
распознавать приведенные квадратные уравнения, приводить примеры;
определять способы решения систем линейных уравнений, решать системы способом подстановки;
решать системы линейных уравнений способом сложения, подстановки.

знать:

определение квадратного уравнения;
какое уравнение называется неполным квадратным уравнением; способы решения неполных квадратных уравнений;
что называется дискриминантом квадратного уравнения, формулу дискриминанта;
как зависит число корней от дискриминанта;
формулу корней квадратного уравнения;
теорему Виета и обратную теореме Виета;
какие уравнения называются приведенными квадратными уравнениями;
алгоритм решения систем линейных уравнений способом подстановки;
алгоритм решения систем уравнений способом сложения;
способы решения уравнений высших степеней.

Краткие теоретические и учебно-методические материалы по теме практической работы

Необходимость решать уравнения не только первой, но и второй степени еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики.

Определение

Уравнение вида ax² + bx + c = 0, где a, b, c - действительные числа, причем a ≠ 0, называют квадратным уравнением.
Если a = 1 , то квадратное уравнение называют приведенным; если a ≠ 1, то неприведенным.

Числа a, b, c носят следующие названия: a - первый коэффициент, b - второй коэффициент, c - свободный член.
Корни уравнения ax² + bx + c = 0 находят по формуле:

Формула

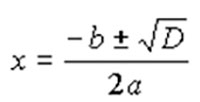
Выражение D = b² - 4ac называют дискриминантом квадратного уравнения.

если D < 0, то уравнение не имеет действительных корней;
если D = 0, то уравнение имеет один действительный корень;
если D > 0, то уравнение имеет два действительных корня.

В случае, когда D = 0, иногда говорят, что квадратное уравнение имеет два одинаковых корня.

Пример:

Уравнение с двумя одинаковыми корнями

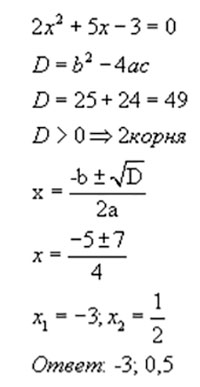
Если в квадратном уравнении ax² + bx + c = 0 второй коэффициент b или свободный член c равен нулю, то квадратное уравнение называется неполным

Неполные уравнения выделяют потому, что для отыскания их корней можно не пользоваться формулой корней квадратного уравнения - проще решить уравнение методом разложения его левой части на множители.

Способы решения неполных квадратных уравнений:

1. c = 0, то уравнение примет вид ax² + bx = 0.
x(ax + b) = 0, x = 0 или ax + b = 0, x = -b : a.

2. b = 0, то уравнение примет вид ax² + c = 0,
x² = -c / a,
x_1,2 = ±√(-c / a).

3. b = 0 и c = 0 , то уравнение примет вид ax² = 0, x = 0

Пример:

Пример уравнения

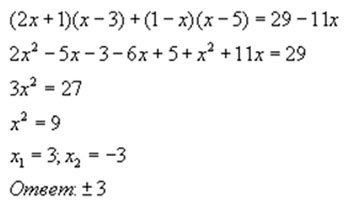
Теорема Виета

Зависимость между корнями и коэффициентами квадратного уравнения выражает теорема Виета. Пусть х₁ и х₂ – корни квадратного уравнения ах² + bх + с = 0, тогда х₁ + х₂ = – b/a, х₁х₂ = c/a. Для приведенного квадратного уравнения х² + рх + q = 0, если х₁ и х₂ – корни этого уравнения, то х₁ + х₂ = – p, х₁х₂ = q.

Справедливо утверждение, обратное теореме Виета: если числа m и n таковы, что их сумма равна – р, а произведение равно q, то эти числа являются корнями уравнения х² + рх + q = 0.

Существуют различные приемы решения систем уравнений

Метод подстановки заключается в следующем:

Одно из уравнений системы преобразуют к виду, в котором y выражено через х (или х через y);
Полученное выражение подставляют вместо y (или вместо х) во второе уравнение. В результате получается уравнение с одной переменной;
Находят корни этого уравнения;
Воспользовавшись выражением y через х (или х через y), находят соответствующие значения х (или y).

Метод сложения основан на следующих теоремах:

Пусть дана система двух уравнений с двумя переменными. Если одно уравнение системы оставить без изменения, а другое уравнение системы заменить уравнением, ему равносильным, то полученная система будет равносильна заданной;
Пусть дана система двух уравнений с двумя переменными. Если одно уравнение системы оставить без изменения, а другое уравнение заменить суммой или разностью обоих уравнений системы, то полученная система будет равносильна заданной.

Метод введения новых переменных применяется при решении систем двух уравнений с двумя переменными одним из следующих способов:

Вводится одна новая переменная только для одного уравнения системы;
Вводятся две новые переменные сразу для обоих уравнений.

Для того чтобы графически решить систему двух уравнений с двумя переменными, нужно в одной системе координат построить графики уравнений и найти координаты точек пересечения этих графиков.

Задания для практического занятия

Задание 1

Краткий опрос:

1) Решить уравнения:
а) х² = 11;
б) х² = – 8;
в) 7х² = 0;
г) х² – 5х = 0.

2) Рассмотреть квадратные уравнения:
a) 2x² + 5x – 7 = 0
б) 3x² – 8x = 0
в) 3x² – 48 = 0
г) 2х² = 0
Чем эти уравнения отличаются друг от друга? (В уравнениях б, в, г отсутствует один из членов). Как называются эти уравнения? (Неполными квадратными уравнениями)

3) Составить квадратное уравнение имеющее корни:
• 3 и –3
• 0 и 6

Задание 2

§20, Стр. 131, Ю.М. Колягин и др., Алгебра и начала анализа. 10 кл. (Учебники выдает преподаватель)
Работа по учебнику.

а) Прочитать материал стр. 131-134. Записать задачи 1, 3 и 4 себе в тетрадь. Работа в парах. Вопросы друг другу и преподавателю.
б) Задачу 6 разобрать у доски. Обсуждение. Записать решение в тетрадь.

Задание 3

Самостоятельно выполнить задания (с проверкой у доски – несколько человек) № 460(1), 462(1), 463(1), 465(1), 470(1)

Задание 4

Сделать самостоятельно № 460(2), 462(2), 463(2), 465(2). Дополнительно (индивидуально) тем, кто быстрее справится с заданиями: № 470(2). Обсудить и проверить решения друг с другом.

Задание 5

§21, Стр. 136, Ю.М. Колягин и др., Алгебра и начала анализа. 10 кл. (Учебники выдает преподаватель)
Работа по учебнику.

а) Прочитать материал стр. 137-140. Записать задачи 1, 2 и 3 себе в тетрадь. Работа в парах. Вопросы друг другу и преподавателю.
б) Задачу 6 разобрать у доски. Обсуждение. Записать решение в тетрадь.

Задание 6

Самостоятельно выполнить задания (с проверкой у доски – несколько человек) № 471-474(1), 477(1), 478(1).

Задание 7

Сделать самостоятельно № 471-474(2), 477(2). Дополнительно (индивидуально) тем, кто быстрее справится с заданиями: № 478(2). Обсудить и проверить решения друг с другом.

Задание 8

§22, cтр. 141, Ю.М. Колягин и др., Алгебра и начала анализа. 10 кл. (Учебники выдает преподаватель)

Работа по учебнику.

а) Прочитать материал стр. 141-150. Записать задачи 1 и 2. Работа в парах. Вопросы друг другу и преподавателю.
б) Задачи 6 и 7 разобрать у доски. Обсуждение. Записать решение в тетрадь.

Задание 9

Самостоятельно выполнить задания (с проверкой у доски – несколько человек) № 480(1), 481(1), 483(1), 492(1).

Задание 10

Сделать самостоятельно № 480(2), 481(2), 483(2). Дополнительно (индивидуально) тем, кто быстрее справится с заданиями: № 492(2). Обсудить и проверить решения друг с другом.

Задание 11
Самостоятельно выполнить задания (по вариантам).

Решите приведенные квадратные уравнения с помощью теоремы Виета