Математические этюды как средство формирования познавательной активности учащихся в урочной и внеурочной деятельности

В процессе учения и познания окружающей действительности принимают участие все органы чувств.

Применение наглядных и технических средств обучения способствует эффективному усвоению информации, активизации познавательной деятельности учащихся, развитию способности связывать теорию с практикой и с жизнью, формированию навыка технической культуры, повышению интереса к обучению.

Проект "Математические этюды" развивает уникальные российские традиции в области естественно-научной популяризации, представляя в увлекательной форме решенные и нерешенные математические задачи, рассказывает как о математической "составляющей" крупнейших достижений цивилизации, так и о математической "начинке" привычных вещей. Основное наполнение – короткометражные фильмы, выполненные с использованием трехмерной компьютерной графики, позволяющей показать красоту математики.

Проект реализуется в стенах Математического института им. В. А. Стеклова РАН с 2002 г. Ежегодно коллекция видеофильмов пополняется. В настоящее время проект содержит 58 фильмов, 38 миниатюр и 31 модель на темы из самых разных разделов математики и ее приложений. Фильмы рассказывают не только о математических идеях, но и о приложениях к технике, об истории рассматриваемых вопросов, ученых и инженерах, принимавших участие в их решении. К каждому фильму прилагается научно-популярный рассказ о том, что люди видят в фильме, а также список литературы, чтобы заинтересовавшиеся школьники могли продолжить изучение этого предмета.

Сайт проекта "Математические этюды"

При обучении математике учитель в своей работе может использовать различные математические этюды и миниатюры как на этапе объяснения нового материала, так и на этапах обобщения и закрепления изученного. Так геометрическая интерпретация алгоритма Евклида о нахождении наибольшего общего делителя двух чисел будет интересна уже пятиклассникам.

На первых уроках геометрии можно предложить учащимся аксиому о трех точках, единственным образом определяющих плоскость. Неразрешимую в Евклидовой геометрии задачу о трисекции угла можно решить с помощью шарнирного механизма построенного на основе параллелограмма. Из этого же сюжета учащиеся узнают о существовании точки бифуркации и антипараллелограмма. Кто знает, возможно, кто-то даже решит построить данный механизм (чертежи прилагаются).

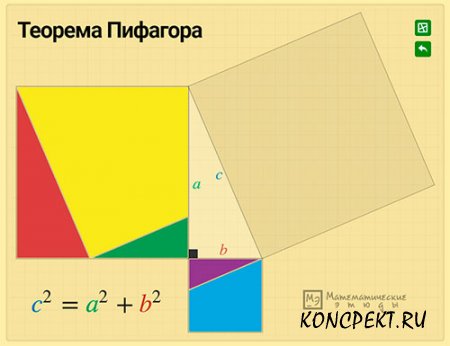
Интерактивная головоломка "Теорема Пифагора" поможет ученикам разобраться с одним из наглядных способов доказательства знаменитой теоремы.

Интерактивная головоломка "Теорема Пифагора"

Понять принцип вычисления площади фигур, ограниченных произвольной замкнутой кривой поможет одноименный этюд. Формула Пика для вычисления площади фигуры на клетчатой бумаге будет интересна как пятиклассникам, так и выпускникам (в КИМах ЕГЭ присутствуют подобные задачи).

Для демонстрации преобразований пространства имеется сюжет Сдвиг и поворот. Во внеурочной деятельности по математике можно предложить ребятам этюд Арифметика Магницкого – в нем рассказывается история первого российского учебника математики, вышедшего в 1703 году при непосредственном участии императора Петра I.

В старших классах можно изучить правила измерения с помощью штангенциркуля и вычисления с помощью логарифмической линейки. При изучении симметрии можно предложить учащимся красочный этюд Калейдоскоп, в котором рассказывается о том, что устройство знакомой с детства игрушки полностью определяется математикой и волшебные узоры поддаются математическому объяснению и описанию.

Во внеурочной деятельности или факультативно можно рассмотреть этюды о кривых постоянной ширины:

• Круглый треугольник Рело;
• Сверление квадратных отверстий;
• Изобретая колесо.

Изучение стереометрии в школе осложнено тем, что изобразить объемное тело на плоской доске не всегда возможно, зачастую трудоемко и требует больших затрат времени. Современные ИКТ-технологии и компьютерная графика в полной мере решают эту проблему. Внутренняя геометрия многогранников представлена множеством разнообразных этюдов.

В одном из них (И это развертка?!) показан необычный способ получения развертки привычных для нас многогранников с помощью нескольких разрезаний и "наматывания" полученной фигуры на многогранник. Этюд Кубисткий паркет демонстрирует, что любую из одиннадцати разверток куба можно использовать для создания паркета (т.е. замостить ими всю плоскость).

Этюд "Кубисткий паркет"

Кусочно-гладкое вложение многогранника – новое направление в геометрии будет особенно интересно будущим архитекторам и модельерам. В ролике демонстрируется как из обычных куба, тетраэдра, цилиндра получить необычные замкнутые тела, границы которых будут состоять не из кусочков плоскостей, а из кусочков гладких поверхностей.
Гармония правильных многогранников не оставит равнодушными ни одного ученика. В видео ролике представлены как сами правильные многогранники, так и их объединения и пересечения.

Удивительные объемы многогранников – видеоролик о том, что из одних и тех же граней могут быть собраны как выпуклые, так и невыпуклые многогранники, вычисляется отношение объемов выпуклого и невыпуклого октаэдров. Но вопрос о максимальном отношении объемов остается открытым и ждет своего исследователя! Соотношения объемов шара и описанного около него цилиндра определил еще в 2 веке до н.э. Архимед.

В сюжете Весы Архимеда наглядно представлена найденная им математическая зависимость. Понять практическую значимость формул площади круга и объема шара и умения их применять поможет сюжет Объем шара о компьютерном CD-диске и апельсине.

При изучении темы "Последовательности" учащимся можно предложить сюжет Бесконечная лестница, который пытливые умы заставит задуматься о возможности ее построения. Другой сюжет с помощью дрели и шестеренок позволяет "ощутить" свойства убывающей геометрической прогрессии.

В статье рассмотрены лишь некоторые этюды, полная же коллекция содержит кроме того 38 миниатюр и 31 модель, которые несомненно станут изюминкой любого урока математики и будут способствовать развитию познавательного интереса обучающихся к изучению математики и служить рекламой математического образования в целом.