Внимание, головоломка!

Для успешного освоения программы школьного обучения ребенку необходимо не только много знать, но и уметь логически мыслить.

Задача развития познавательных способностей детей может быть решена только в том случае, если ей будут подчинены и содержание, и методы учебной работы.

Большое значение имеет подбор таких заданий для занятий математикой, которые требовали бы от детей проведения самостоятельных наблюдений, сравнения, описания рассматриваемых явлений, описания выполнения действий.

Особый интерес представляет головоломка о расстановке цифр: "Нарисуй такие кружки и заполни их различными нужными цифрами от 1 до 9 так, чтобы сумма чисел по каждой стороне "треугольника" была равна 20, равна 17".

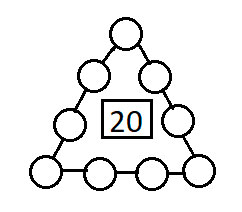
При решение этой головоломки возникает целый ряд вопросов, ответы на которых не так просты:

• Почему сумма чисел по каждой стороне треугольника 17 и 20, а не 18 и 22?
• Может ли сумма чисел по каждой стороне треугольника быть равной 16? 19? 24?
• Если расстановка цифр по сторонам треугольника возможна, то она единственна или нет?
• Любые ли 3 цифры можно записать в вершинах треугольника?
• Как упростить поиск решения?

В данной статье ответим на вопросы по решению данной головоломки.

1. Узнаем возможные значения для сумм по каждой стороне треугольника при расстановке цифр от 1 до 9:

а) наименьшая сумма получится, если в вершинах треугольника записаны цифры 1, 2, 3. Сумма всех чисел от 1 до 9 равна 45; сумма чисел по трем сторонам треугольника равна 45+1+2+3=51, так как числа, стоящие в вершинах, суммируются дважды, сумма чисел по каждой стороне треугольника равна 51:3=17. 17 - наименьшая возможная сумма чнтырех чисел по каждой стороне треугольника.

б) наибольшая сумма получится, если в вершинах "треугольника" записаны цифры 7, 8, 9. Сумма чисел по трем сторонам "треугольника" равна 45+7+8+9=69, сумма чисел по каждой стороне "треугольника" равна 69:3=23, 23 - наибольшая возможная сумма четырех чисел по каждой стороне "треугольника".

Возможные значения сумм по каждой стороне "треугольника": 17, 18, 19, 20, 21, 22, 23. При проверке убеждаемся, что головоломка имеет решение для чисел 17, 19, 20, 21 и 23; сумма чисел по каждой стороне треугольника.

Не может быть равна 18 и 22; в некоторых случаях решение неоднозначно. (таблица)

Ответ. Из цифр 1, 2, 3, 4, 5, 6, 7, 8, 9 составить 84 неупорядоченных тройки. Из расположения троек можно заменить способ их выписывания. Цветом выделены тройки цифр, сумма чисел которых делится на 3.

Всего 84.

2. Некоторые рекомендации по решению головоломки.

Работа с условием головоломки

• Назови и покажи числа в порядке возрастания, записанные в кружках. Что ты заметил? (в кружках записаны все цифры от 1 до 9)
• Назови числа по каждой стороне "треугольника".
• Найди сумму чисел по каждой стороне "треугольника" что ты заметил?

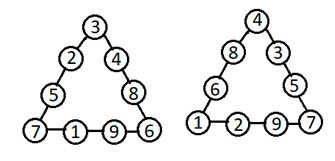
(на перром рисунке суммы чисел по каждой стороне "треугольника" разные, на втором – все суммы равны одному и тому же числу)

Назови числа, записанные в вершинах "треугольника". Вычисли сумму этих чисел для каждого "треугольника", сравни суммы. Чем они отличаются? (16 и 12, 12 делится на 3, 16 не делится на 3)

Подготовительная работа

• Какие цифры из промежутка от 1 до 9 надо записать в пустые кружки? Каждая цифра должна быть записана только один раз (4, 7 и 8).
• Расставить цифры 4, 7 и 8 в пустые кружки так, чтобы сумма чисел по каждой стороне 2 треугольника" была равна 21.

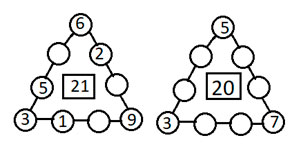
Продолжи заполнение кружков различными цифрами из промежутка от 1 до 9 так, чтобы сумма чисел по каждой стороне "треугольника" была равна 20. (По каждой стороне "треугольника" записаны числа 8=3+5, 10=3+7, 12=5+7, остается дополнить эти числа до 20)

Других способов расстановка цифр 1, 2, 6, 8, 9, 4 нет.

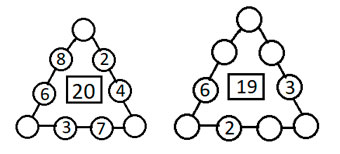
Продолжи заполнение кружков (рис.6) от 1 до 9 так, чтобы сумма чисел по каждой стороне "треугольника" была равна 20 Цифры не должны повторяться. (В вершинах "треугольника" надо расставить цифры 1, 5, 9. Суммы двух чисел по каждой стороне равна 14,6 и 10. Остается записать дополнения этих чисел до 20, т.е. 6=1+5, 10=1+9, 14=9+5)

Продолжи заполнение кружков цифрами от 1 до 9 так, чтобы цифры не повторялись, и чтобы сумма чисел по каждой стороне "треугольника" была равна 19. (Сумма чисел в вершинах "треугольника" равна 12, из таблицы находим тройку цифр (1, 4, 7), подбираем другие цифры и т. д.)

Увеличить каждое число, записанное по стороне "треугольника", в 5 раз. Во сколько раз увеличится сумма чисел по каждой стороне "треугольника"? Проверь, на сколько увеличится сумма чисел по каждой стороне "треугольника"

Запиши в пустые кружки такие цифры из промежутка от 1 до 9, чтобы все цифры по сторонам "треугольника" были различными и суммы чисел по каждой стороне "треугольника" были равны одному и тому же числу. (Так как в вершинах "треугольника записаны цифры 1, 2, 3, то сумма чисел по каждой стороне "треугольника равна 17)

Поменяй местами две цифры так, чтобы суммы чисел по каждой стороне "треугольника" были равны. (В первом треугольнике надо поменять местами цифры 3 и 7, во втором – цифры 2 и 3)

Заполни кружки различными цифрами от 1 до 9 так, чтобы суммы чисел по каждой стороне были соответственно равны 18, 19 и 20.

Рисунок 5

В ходе решения данных головоломок дети учатся планировать свои действия, обдумывать поиск результатов. Эта работа активизирует и мыслительную деятельность детей.