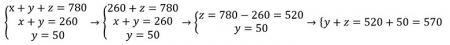Решение демонстрационного варианта теоретической части ОГЭ по информатике

В работе приводится пример решение демонстрационного варианта теоретической части ОГЭ по информатике (2022 год), включающий 10 заданий с правильными ответами.

Задания теоретической части ОГЭ по информатике

Задание 1

В одной из кодировок Unicode каждый символ кодируется 16 битами. Ученик написал текст (в нем нет лишних пробелов): Ёж, лев, слон, олень, тюлень, носорог, крокодил, аллигатор - дикие животные.

Ученик удалил из списка название одного предмета, а также лишние запятую и пробел - два пробела не должны идти подряд. При этом размер нового предложения в данной кодировке оказался на 16 байт меньше, чем размер исходного предложения. Напишите в ответе вычеркнутое название животного.

Решение:
1. Для начала определим сколько символов удалили всего(вместе с запятой и пробелом). Так как один символ кодируется 16 битами, то переведем биты в байты 16 бит = 16:8=2 байта. Следовательно, чтобы узнать сколько символов удалили необходимо общее количество байт (16 байт) разделить на количество байт, которые приходятся на один символ (2 байта). Тогда получится 16 : 2 = 8 символов удалили.

2. Теперь подсчитаем количество символов в удаленном слове. Для этого необходимо от общего количества символов отнять 1 пробел и 1 запятую т.е. 8 - 1 - 1 = 6 символов содержит удаленный предмет (животное).

3. Из приведенного выше предложения выбираем животное, которое содержит 6 символов - это тюлень.

Ответ: тюлень.

Задание 2

От разведчика было получено следующее сообщение: 001001110110100
В этом сообщении зашифрован пароль - последовательность русских букв. В пароле использовались только буквы А, Б, К, Л, О, С; каждая буква кодировалась двоичным словом по следующей таблице.

А	Б	К	Л	О	С
01	100	101	111	00	110

Расшифруйте сообщение. Запишите в ответе пароль.

Решение:

1. Выписываем сообщение. (делаем для того, чтобы если допустим ошибку, чтобы исправить)

2. Приступаем к расшифровке. Смотрим на таблицу: в ней каждая буква зашифрована двумя цифрами либо тремя. Мы соответственно начинаем проверять сообщение с двух цифр если две цифры не походят, то берем три цифры:

00	100	111	01	101	00
О	Б	Л	А	К	О

Ответ: облако.

Задание 3

Напишите наименьшее число x, для которого истинно высказывание: (x > 16) И НЕ (x нечетное).

Решение:
В данном высказывании четыре логических действия: два действия в скобках, логическое отрицание (НЕ), логическое умножение (И).

1. Посмотрим на высказывание и определим, чтобы все высказывание было истинным необходимо, чтобы оба составных высказываний было истинными, а для этого необходимо: высказывание х > 16 истинно, когда х = 17, 18, 19,20, 21, 22, ..., высказывание НЕ (х четное) преобразуем т.е., чтобы оно было истинным нужно, чтобы просто x было нечетным или х = 1, 3, 5, 7, 9. 11, 13, 15, 17, 19, 21, 23 ...

2. Смотрим внимательно какие значения х нам подходят и видим, что это 17, 19, 21, 23 и т.д. Следовательно наименьшее значение х это 17.

Ответ: 17.

Задание 4

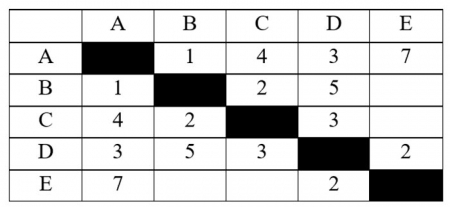
Между населенными пунктами A, B, C, D, E построены протяженность которых (в километрах) приведена в таблице.

Таблица с расстояниями между населенными пунктами

Определите длину кратчайшего пути между пунктами A и Е, проходящего через пункт С. Передвигаться можно только по дорогам, протяженность которых указана в таблице. Каждый пункт можно посетить только один раз.

Решение:

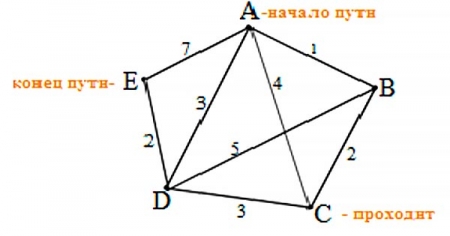
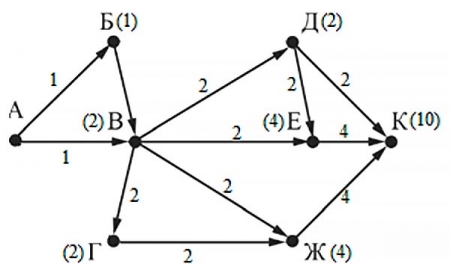
1. Данную задачу будем решать графически т.е. отметим пункты точками не лежащими на одной прямой и соединим их дорогами данные по которым представлены в таблице.

Графическое решение задачи

2. Отмечаем все возможные пути из пункта А в пункт Е и проходящих через пункт С.

Все возможные пути из А в Е, проходящие через С

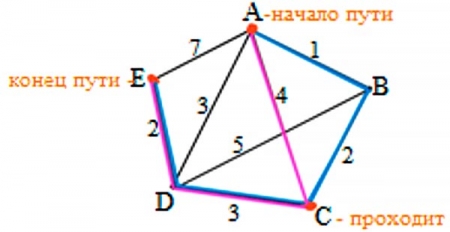
по рисунку видно, что из пункта А в пункт В через С ведут всего две дороги отмечены синим и красным цветом. Подсчитаем длины данных путей:

• путь АВСDE = 1+2+3+2=8
• путь АСDE=4+3+2=9

Так как самый короткий путь АВСDE=8, то Ответ: 8

Задание 5

У исполнителя Альфа две команды, которым присвоены номера:

1. прибавь 1.
2. умножь на b. (b - неизвестное натуральное число; b > 2)

Первая из них увеличивает число на экране на 1, вторая умножает его на b. Алгоритм для исполнителя Альфа - это последовательность номеров команд. Найдите значение числа b, при котором из числа 6 по алгоритму 11211 будет получено число 82.

Решение:

1. Дано число 6, необходимо выполняя последовательно команды 11211 получить число 82.

2. Составим выражение применяя команды 11211 и решаем как уравнение: (6+1+1)*b+1+1=82
8*b+2=82
b=10

Ответ: 10.

Задание 6

Ниже приведена программа, записанная на трех языках программирования.

Было проведено 9 запусков программы, при которых в качестве значений переменных вводились следующие пары чисел (s, t): (1, 2); (11, 2); (1, 12); (11, 12); (-11, -12); (-11, 12); (-12, 11); (10, 10); (10, 5). Сколько было запусков, при которых программа напечатала "YES"?

Решение:

Разберем решение данной задачи используя программу на языке Pascal. Нам необходимо поочередно ввести пары чисел (1,2) до (10,5) в программу, первое число вместо переменной s, второе число вместо переменной t, и посчитать сколько раз выражение (s > 10) or (t > 10) будет истинно, то это соответственно и будет ответом.

Рассмотрим выражение (s > 10) or (t > 10), по закону логики "выражение истинно тогда и только тогда когда хотя бы одно из высказываний истинно" (потому что or - это логическая функция "или"), проверим первую пару (1,2): подставим вместо s первое число, а вместо t второе число, получим (1>10) or (2>10) - выражение ложно так как оба высказывания ложны;

проверим вторую пару (11, 2): также подставим вместо s и t: (11>10) or (2>10) - выражение истинно так как истинна первое высказывание. Таким же образом проверяем и остальные пары, получается что истину или ответ "YES" обеспечат пары (11, 2); (1, 12); (11, 12); (-11, 12); (-12, 11) - всего пять. Следовательно ответ пять пар.

Ответ: 5.

Задание 7

Доступ к файлу rus.doc, находящемуся на сервере obr.org, осуществляется по протоколу https. Фрагменты адреса файла закодированы цифрами от 1 до 7. Запишите в ответе последовательность этих цифр, кодирующую адрес указанного файла в сети Интернет: 1) obr. 2) / 3) org 4) :// 5) doc 6) rus. 7) https

Решение:

Соберем фрагменты файла и запишем полный путь к файлу указанного в сети интернет: адрес в сети интернет начинается с протокола, затем сервер, а потом могут идти каталоги и файлы. Следовательно адрес файла: https://obr.org/rus.doc. Осталось только выписать цифры соответствующие каждому фрагменту файла (незабываем про слеш "/", он разделяет файлы, каталоги и сервера).

Ответ: 7413265.

Задание 8

В языке запросов поискового сервера для обозначения логической операции "ИЛИ" используется символ "|", а для обозначения логической операции "И" - символ "&".В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

Какое количество страниц (в тысячах) будет найдено по запросу Рыбка? Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Решение:

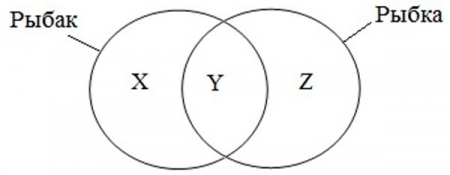
Для решения данной задачи воспользуемся кругами Эйлера-Вена и составим систему уравнений:

Круги Эйлера-Вена

Используя данные таблицы составим систему уравнений для решения поставленной задачи, в 1 условии запроса Рыбак | Рыбка означает, что необходимо сложить все области, где упоминается Рыбак, Рыбка, а также Рыбак и Рыбка вместе, получаем x+y+z=780.

Во 2 условии запрос Рыбак, смотрим на круг - это две области x + y = 260, в 3 условии Рыбак & Рыбка - это пересечение, т.е. область, где встречается и Рыбак и Рыбка, а это y=50. И последнее, что необходимо найти по запросу Рыбка - это две области y+z=? В итоге получаем:

Система уравнений

Ответ: 570.

Задание 9

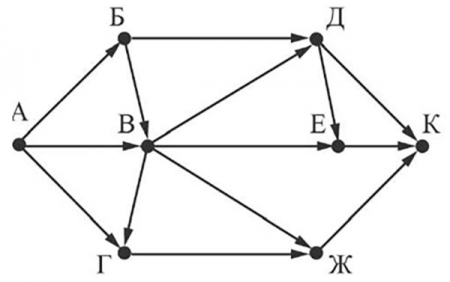
На рисунке - схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж и К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К, проходящих через город В?

Схема дорог

Решение:

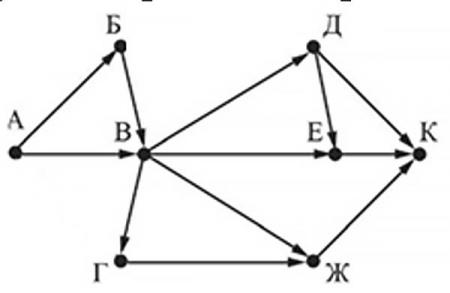
Анализируя данные задачи необходимо убрать маршруты через которые не будем проходить по условию задачи, а это из А в Г, из Б в Д (так как оба маршрута не проходят через В), получаем:

Схема без маршрутов, по которым не будет проходить путь

Осталось только построить маршруты и подсчитать их количество:

Построение маршрутов

Таким образом количество маршрутов из пункта А в пункт К, проходящих через пункт В равно 10.

Ответ: 10.

Задание 10

Среди приведенных ниже трех чисел, записанных в различных системах счисления, найдите максимальное и запишите его в ответе в десятичной системе счисления. В ответе запишите только число, основание системы счисления указывать не нужно.
23₁₆, 32₈, 11110₂.

Решение:

Вариант решения очень прост, необходимо перевести числа из шестнадцатеричной, восьмеричной и двоичной системы счисления (об системе счисления говорят индексы у чисел 16, 8 и 2) в десятичную, затем сравнить и выписать наибольшее. Перевод осуществляем следующим способом:

1. Над каждым числом на пишем степени в которые будем возводить основания системы:
10   10    43210
23₁₆, 32₈, 11110₂

2. Выпишем каждое число в развернутом виде, т.е. берем число умножаем его на основание, которое в свою очередь необходимо возвести в степень подписанное над числом, затем прибавляем следующее число умноженное на основание возведенное в степень и так до тех пор пока не закончатся числа, затем полученные произведения складываем:

23₁₆=2*16¹+3*16⁰=32+3=35
32₈=3*8¹+2*8⁰=24+2=26

11110₂=1*2⁴+1*2³+1*2²+1*2¹+0*2⁰=16+8+4+2=30
Наибольший результат 35.

Ответ: 35.

informatika.rar

Размер:

100.97 Kb

Скачали:

16