Использование метода динамического программирования при решении задания № 15 ЕГЭ по информатике

Динамическое программирование — способ решения сложных задач путем разбиения их на более простые подзадачи. Он применим к задачам с оптимальной подструктурой, выглядящим как набор перекрывающихся подзадач, сложность которых чуть меньше исходной.

В данной статье показано, как метод динамического программирования можно успешно применить при решении задач на подсчет путей в графе при решении задания № 15 ЕГЭ по информатике.

Задание № 1

Рассмотрим на примере конкретную задачу поиска количества путей в графе. Это задание № 15 ЕГЭ по информатике.
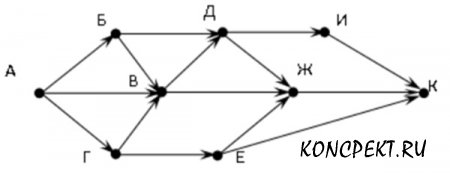
На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?

Схема дорог

Первое, что приходит в голову – это пересчитывать количество путей вручную, начиная с вершины А и заканчивая вершиной К. Используя этот метод легко допустить ошибку и запутаться в подсчете.

Чтобы не ошибиться в расчетах будем записывать количество путей для каждой вершины в таблицу (см. таб. 1). Для вершины A есть один способ оставаться в ней и никуда не идти. Запишем число 1 в столбец А. В вершину Б мы можем попасть только из вершины А (смотрим на стрелку). Значит, число способов попасть в вершину Б равно 1. В город В можно попасть из города А, Б или Г. (см. на стрелки, входящие в вершину В)

Количество путей для вершин А и Б уже было рассчитано. Чтобы определить количество способов попасть в город В, определим число способов попасть в Г. В вершину Г можно попасть только из А. Следовательно, количество способов попасть в город В=А+Б+Г=1+1+1=3. В вершину Д можно попасть из Б или из В. Количество способов для вершины В мы уже рассчитали, поэтому количество способов попасть в Д=Б+В=1+3=4.

В город Е можно попасть только из города Г, поэтому поставим в этом столбце число 1. В город Ж можно попасть из Д, из В, либо из Е. Для вершины Д количество способов мы уже рассчитали (4 способа), для вершины В – 3 способа и для Е – 1 способ. Значит, количество способов попасть в город Ж=4+3+1=8. В город И можно попасть только из города Д, а значит число способов попасть в город И равно 4. Наконец, в вершину К можно попасть из И, Ж или Е. Просуммируем уже рассчитанные способы для этих вершин.

Следовательно, общее количество способов попасть из города А в город К равно 13.
Ответ: 13.

Итак, в чем выражается метод динамического программирования? Мы показали, как из решения подзадач формируется решение исходной задачи. Причем, каждую подзадачу мы решали только один раз, запоминая промежуточные результаты в таблицу.

Разберем несколько примеров, где может быть использован описанный метод.

Задание № 2

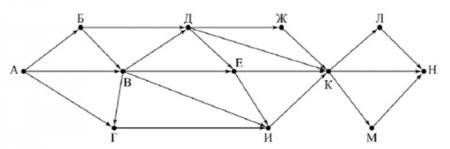
На рисунке - схема дорог, связывающих пункты А, Б, В, Г, Д, Е, Ж, И, К, Л, М, Н. Сколько существует различных путей из пункта А в пункт Н, не проходящих через пункт Е?

Граф к заданию 2

Решение:
Задание № 2 будем также решать методом динамического программирования. Построим таблицу, в которую будем записывать количество возможных путей для каждой вершины. До вершины Е идем согласно заданию №1. Так как по условию задания нам следует исключить пути, проходящие через пункт Е, то для этой вершины не будем считать количество путей. Проще всего в таблицу в столбец Е поставить число 0. Для остальных вершин правило заполнения таблицы не изменится. (см. таб. 2)

Заполнив таблицу, получим количество путей из пункта А в пункт Н, равное 33.
Ответ: 33.

Задание № 3

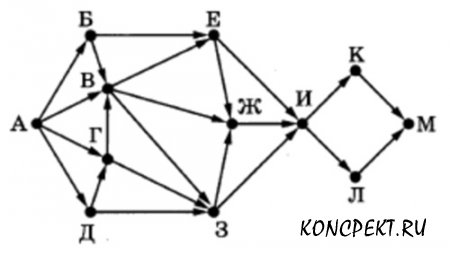
На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, 3, И, К, Л, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город М, проходящих через город Л, но не проходящих через город Е?

Схема дорог связывающих города

Решение:

Эта задача решается также, используя метод динамического программирования. Построим таблицу, в которую будем вписывать количество путей для очередной вершины. Количество путей, ведущих в вершину Е, обнулим (как в предыдущем задании). Так как пути должны обязательно проходить через город Л, то следует обнулить количество путей для вершины К (см. Таб. 3)

Ответ: 18.
Итак, метод динамического программирования может с успехом применяться при решении заданий на подсчет количества путей в графе.