Исследовательская работа по физике на тему "Физика в пружине"

С точки зрения классической физики, пружину можно рассматривать как устройство, накапливающее потенциальную энергию путем изменения расстояния между атомами эластичного материала.

В теории упругости законом Гука установлено, что растяжение эластичного стержня пропорционально приложенной к нему силе, направленной вдоль его оси. В реальности этот закон выполняется не точно, а только при малых растяжениях и сжатиях.

Если напряжение превышает определенный предел (предел текучести) в материале наступают необратимые нарушения его структуры, и деталь разрушается или получает необратимую деформацию. Следует отметить, что многие реальные материалы не имеют четко обозначенного предела текучести, и закон Гука к ним неприменим. В таком случае, для материала устанавливается условный предел текучести.

Витые металлические пружины преобразуют деформацию сжатия/растяжения пружины в деформацию кручения материала, из которого она изготовлена, и наоборот, деформацию кручения пружины в деформацию растяжения и изгиба металла, многократно усиливая коэффициент упругости за счет увеличения длины проволоки противостоящей внешнему воздействию. Волновые пружины сжатия подобны множеству последовательно/параллельно соединенных рессор, работающих на изгиб.

В текущем времени развития пружина используется во многих механизмах, к примеру, в автомобиле, в механизмах.

Объект исследования: пружина.

Предмет исследования: физические свойства пружины.

Цель исследования: изучить историю возникновения пружины и ее свойства.

Задачи исследования:

1. Изучить свойства пружины.
2. Разобрать закон Гука.

Вывод по результатам исследования: деформация пружины по закону Гука, будет пропорциональна удлинению тела, и при добавлении новых одинаковых по весу грузов, будет растягивать пропорционально пружину. В зависимости от разной нагрузки на пружину, деформация, возникающая в упругом теле, пропорциональна приложенной к этому телу силе.

Основная часть

Описание и анализ проблемной ситуации

Пружина различных механизмов, накапливающий и отдающий, или поглощающий механическую энергию - упругий элемент машин и

Закон Гука - утверждение, согласно которому, деформация, возникающая в упругом теле (пружине, стержне, консоли, балке и т. д.), пропорциональна приложенной к этому телу силе. Открыт в 1660 году английским ученым Робертом Гуком.

История создания и законы пружины

Сегодня существуют пружины растяжения, сжатия, изгиба и кручения. Все они объединяются тем, что в них используется сила упругости материала. Под воздействием силы, приложенной извне, она изменяет свою форму, а потом принимает прежнюю форму, воздействуя на соседние детали.

Пружины использовались людьми с незапамятных времен. В первую очередь, конечно, в оружии. Древние луки изготавливались из дерева или рога животных. Прочность и упругость этих материалов была достаточной, чтобы метко пущенная стрела оказалась смертельной.

В третьем веке до нашей эры греческий инженер Ктесибий из Александрии изобрел способ производства, за счет увеличения доли олова в медном сплаве. Бронза сначала отливалась, а затем упрочнялась ударами молотка.

Другое существенное событие в истории пружин произошло в Средние века. Мотопила, разработанная Вилларом де Оннекуром около 1250 года под воздействием водяного колеса, толкала лезвие пилы в одном направлении, одновременно изгибая жердь; когда же жердь разгибалась в свое первоначальное состояние, она тянула лезвие пилы обратно.

Спиральные пружины были изобретены в начале пятнадцатого века. Заменив систему весов, которая обычно заводила часы с механизмом пружины намотки, часовых дел мастера смогли сконструировать надежное портативное средство хронометража. Это позволило отслеживать точную навигацию для кораблей, идущих в океан.

В XVIII веке индустриальная революция подстегнула развитие технологий массового производства для изготовления пружин. В течение восьмидесятых годов восемнадцатого века британский слесарь Джозеф Брама использовал машину намотки пружин на его фабрике. Очевидно, будучи адаптацией токарного станка, машина содержала катушку проволоки вместо режущей головки.

Проволока из катушки накручивалась на стержень, закрепленный на станке. Скорость главного винта, который содержал катушку параллельно вращающемуся стержню, можно регулировать, меняя тем самым промежутки между витками.

Пружина - упругий элемент машин и различных механизмов, накапливающий и отдающий, или поглощающий механическую энергию.

Витая цилиндрическая пружина сжатия или растяжения, намотанная из цилиндрической проволоки и упруго деформируемая вдоль оси, имеет коэффициент жесткости. Для расчета применяется следующая формула: k=Gd⁴/8D³n, где

• G – применяется для определения модуля сдвига. Стоит учитывать, что это свойство во многом зависит от применяемого материала при изготовлении витков.
• d – диаметральный показатель проволоки. Она производится путем проката. Этот параметр указывается также в технической документации.
• D – диаметр создаваемых витков при накручивании проволоки вокруг оси. Он подбирается в зависимости от поставленных задач. Во многом диаметр определяет то, какая нагрузка оказывается для сжатия устройства.
• n – число витков. Этот показатель может варьировать в достаточно большом диапазоне, также влияет на основные эксплуатационные характеристики изделия.

Виды пружин

По виду воспринимаемой нагрузки:

1. пружины сжатия.
2. пружины растяжения
3. пружины кручения.
4. пружины изгиба.

Пружины растяжения - рассчитаны на увеличение длины под нагрузкой. В ненагруженном состоянии обычно имеют сомкнувшиеся витки. На концах для закрепления пружины на конструкции имеются крючки или кольца.

Пружины сжатия - рассчитаны на уменьшение длины под нагрузкой. Витки таких пружин без нагрузки не касаются друг друга. Концевые витки поджимают к соседним и торцы пружины шлифуют. Длинные пружины сжатия, во избежание потери устойчивости, ставят на оправки или стаканы.

Пружины кручения - могут быть двух видов:

• торсионные - стержень, работающий на кручение (имеет большую длину, чем витая пружина);
• витые пружины, работающие на кручение (как в бельевых прищепках, в мышеловках и в канцелярских дыроколах).

Применение пружин в современном мире

Пружины в быту:

• Большей популярностью в быту пользуется пружина растяжения. Обычно пружины растяжения покупают для механизмов, работа которых основана на возвратных движениях. Деталь компенсирует приложенное к ней усилие. Яркий пример – авто возвратная дверь.
• Бытовая мебель, в частности раскладные диваны и некоторые модели кроватей, оснащаются пружинами. Невозможно сосчитать количество окружающих нас приборов, содержащих этот гибкий элемент. В загородных домах, квартирах, технических помещениях и гаражах можно подыскать десятки примеров. Пружины также незаменимы в мелком бытовом ремонте.

Пружины в автомобилях:

Конструкция автомобилей включает десятки пружин. Это не только амортизирующие элементы, но и ряд других узлов. К примеру, для возврата барабанного тормоза используется пружина растяжения. Системы сцепления и газа также оснащаются рядом упругих металлических элементов. Они выполняют функцию возвращения педалей после отбрасывания ноги. Стоит отметить, что нарушение целостности такой небольшой детали, как пружина, может привести к тяжелым последствиям для автолюбителя.

Пружина в оружии:

• Боевая пружина, возвратная пружина, пружина магазина
• В симуляции оружия, оружие для Страйк бола - пружина обычно используется для выталкивания снаряда в пружинно-поршневых винтовках.

Растяжение пружины
Рассмотрим подробнее деформацию растяжения на примере пружины.

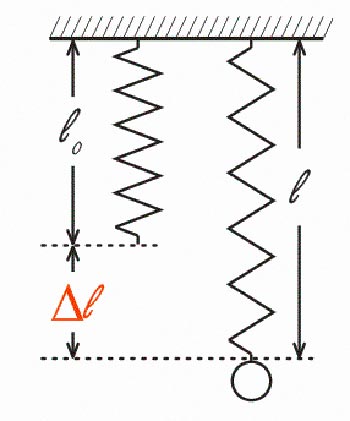
Подвесим теперь к пружине груз. Пружина будет иметь длину L, указанную на рисунке справа. Сравним длину нагруженной пружины с длиной свободно висящей пружины:

L0+ΔL=L

Найдем разницу (разность) между длинами свободно висящей пружины и пружины с грузом. Вычтем для этого из обеих частей этого уравнения величину L0:
ΔL=L-L0

• L0 (м) – начальная длина пружины;
• L (м) – конечная длина растянутой пружины;
• ΔL (м) – кусочек длины, на который растянули пружину.

Иногда рассчитывают относительное удлинение. Это относительное удлинение часто выражают десятичной дробью. Или дробью, в знаменателе которой находится число 100 - такую дробь называют процентом.

Примечание: Отношение – это дробь. Относительное – значит, дробное.
ΔLL0 = L-L0L0 = ε (ε – это отношение (доля) растяжения пружины к ее начальной длине. Измеряют в процентах и называют относительным удлинением)

Закон Гука

Закон Гука - утверждение, согласно которому, деформация, возникающая в упругом теле (пружине, стержне, консоли, балке и т. д.), пропорциональна приложенной к этому телу силе. Открыт в 1660 году английским ученым Робертом Гуком.

Роберт Гук (1635-1703) английский изобретатель

Следует иметь в виду, что закон Гука выполняется только при малых деформациях. При превышении предела пропорциональности связь между напряжениями и деформациями становится нелинейной. Для многих сред закон Гука неприменим даже при малых деформациях.

Если к пружине повесить одну гирьку, тогда пружина деформируется - удлинилась на некоторую величину х . Если к пружине подвесить две одинаковые гирьки, то удлинение стало в два раза больше. Удлинение пружины пропорционально силе упругости.

Сила упругости - это сила, возникающая в теле в результате его деформации и стремящаяся вернуть его в исходное состояние.
Формула расчета силы упругости: F = kx

Исследовательская часть

Этим примером, я исследовал закон Гука. Этот пример эффектно демонстрирует деформацию пружины под весом. Для эксперимента мне понадобился: пружина, линейка, гири весом (1.7 кг)

Цель работы: разобрать действие пружины, на которое действует груз

Использование закона Гука

Пружина в покое и с подвешенной гирей

На рисунке 1 изображено, что пружина в покое не деформировалась, и ее длина составляет 49 см. На рисунке 2 изображено, что при добавлении одного груза, пружина деформировалась, и теперь ее длина составляет 75см. Пружина деформировалась на 26см.

Пружина с двумя гирями

На рисунке 3 было добавлено два одинаковых по весу груза, и теперь пружина деформировалась еще больше и ее длина составляет теперь 101 см, то есть пружина деформировалась еще на 26 см.

И так как каждый раз пружина деформировалась на 26 см, можно определить силу упругости пружины. Коэффициент упругости, Н/м = 100. Удлинение, м = 0.26. В итоге сила упругости H = 26.

Анализ практической части

Сила упругости, возникающая при деформации тела, по модулю пропорциональна удлинению тела и направлена так, что стремится уменьшить величину деформации тела.

Так как закон Гука действует равномерно при одинаковых нагрузках, то если навешать на пружины много грузов, то в какой то момент, пружина уже не сможет деформироваться. И даже уже не сможет вернуть свою первоначальную форму, и из за этого пружина уже не будет пружиной.

Заключение

Изучив теоретический материал, а именно что такое закон Гука, историю создания пружины, виды пружин, применение пружины в современном мире, ее растяжение.

В ходе исследовательской работы, стало известно о принципе пружины. А также влияния груза, на пружину. Определили силу упругости пружины. В рамках своего исследовательского проекта о физике пружины я убедился, что по закону Гука пружина, находящийся в состоянии деформации, стремится восстановить состояние покоя.