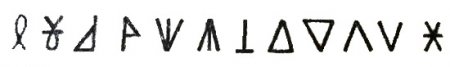Обобщение знаний по математике с помощью "сказочных цифр"

Одна из задач внеклассных занятий по математике - углубление и обобщение тех знаний, которые предусмотрены программой. Для реализации этой задачи можно использовать различные методы, средства и приемы. Одним из таких приемов является занимательность учебного материала.

В данной статье занимательность материала обеспечивается, тем, что учащиеся попадают в сказочную школу, в которой все правила математики такие же, как в обычной школе, но только иначе пишутся цифры.

Эти цифры представляют собой любые несложные по начертанию знаки. Например, такие:

Сказочные цифры

По ходу работы их значения будут произвольно меняться, т.е. один и тот же знак в одном задании может обозначать число 4, а в другом - 7 (ведь это же игра). И произвольность, и условность обозначения цифры имеют важное значение для формирования у учащихся элементов отвлеченного мышления, логически правильных рассуждений и вместе с тем повышения осознанности и обобщенности приобретенных детьми знаний.

Ввести "сказочные числа" можно следующим образом.

Учащимся объявляется, что они отправляются в сказочную школу. В этой школе на уроке математики они видят такую запись:

Учитель предлагает детям догадаться, какое из трех записанных чисел самое большое. Ответ легко дают первоклассники. Учитель радостно подчеркивает, что, хотя числа и неизвестны, дети все же сумели о них кое-что сказать, и для закрепления успеха дает аналогичное задание относительно вычитания.

Итак, условные числа введены. В дальнейшем они часто будут использовать вперемежку с нашими арабскими числами, об этом учитель и сообщает детям. За выполнением задания должно следовать обсуждение решений. Чтобы побудить учащихся давать развернутые объяснения, можно ввести сказочные персонажи (например, ослика Иа или Пятачка), которые часто ошибаются и которым надо растолковывать, а чем состоит их ошибка.

Среди предлагаемых заданий будут встречаться нерешаемые, но которые особенно важны для формирования способности к анализу. В этих случаях оказывает хорошую помощь еще один литературный персонаж – озорник и хитрец Буратино, ставящий ребятам ловушки, которые нужно обнаружить, чтобы не попасться в них. Ко всему этому можно добавить элемент чисто внешней привлекательности.

Так участники занятий получают сказочные дневники (красочные открытки), в которые они наклеивают сказочные отметки – разные геометрические фигуры, вырезанные из красивой, например, бархатной бумаги разных оттенков оранжевого, красного и вишневого цвета. В конце занятий учитель раздает их, поясняя: "Тебе поставлен знак трудолюбия, тебе знак догадливости, тебе знак аккуратности". Важно, чтобы каждый ученик, и особенно тот, который на уроках получает мало похвал, мог украсить свой дневник двумя – тремя яркими знаками.

Отбор конкретных заданий для компоновки конкретного занятия учитель должен сам, учитывая уровень знаний и развития личности своих учащихся.
Затем, сказочные числа я заменяю буквами.

Свойство числового ряда. При освоении числового ряда первоклассники получают представление о его упорядоченности и о том, что соседние числа в ряду различаются на единицу. На этой основе строятся первые вычисления: 4+1=? Ученик 1 класса, выполняя вычисление, должен, примерно, рассуждать так: "Если мы к 4 + 1, значит, должны получить следующее число. Следующее за 4 число - 5, значит, 4+1=5.

Однако услышать такое объяснение от первоклассника почти невозможно. Одна из причин этого заключается в том, что он уже хорошо знает конкретные результаты соответствующих случаев вычислений, и поэтому обращение к числовому ряду, которое требует учитель, у него носит формальный характер.

Предлагаемые задания помогут учащимся осознать смысл обращения к числовому ряду и его важнейшие свойства. Учащиеся говорят, а учитель записывает на доске часть числового ряда от 4 до 8 и от 3 до 9. Это подготовка к работе с частью сказочного числового ряда. Далее учитель записывает 6 знаков, например, В, С, Б, Т, Н, и предупреждает, что эти числа написаны по порядку, так же как только, что были записаны наши числа, причем самое первое число – это не 1, т.к. часть числового ряда взята не с самого начала.

Зная это, требуется определить:

1. самое большое из записанных чисел; (Н)
2. число, меньшее этого самого большого числа на 1; (В)
3. самое маленькое число; (В)
4. число, большее этого маленького числа на 1; (С)
5. на сколько число С меньше числа В; (на 1)
6. на сколько число Б больше числа С; (на 2)

Продолжается работа с тем же отрезком числового ряда. Предлагаю решить примеры, составленные Буратиной. Напоминаю, что Буратино ставит для детей хитрые ловушки, т.е. дает такие задания, ответ к которым не всегда можно найти, и предлагает догадаться, какие же примеры составил Буратино:

С+1=(Р)
Б-1=(Р)
Р+2=(Т)
Н-2=(Б)
Н+1=
В-1=
С-2=

В последних примерах ответа дать нельзя, т.к. в ряду отсутствуют нужные числа.

Вставь пропущенные числа:
С+*=Р
Б-*=Р
Т-*=Р

Вставь пропущенные знаки и числа:
Р**=В
Р**=Б

Дано одно число и оставлены места для других чисел части нового отрезка числового ряда. нужно, рассмотрев примеры, вписать в ряд встречающие в них сказочные числа:

…К… …Б…
К-1=С Н+1=Б
К+ 2=Е Р-2=Б
Е-1=Н Г+1=Р

В этом случае пример начинается с искомого числа, а заканчивается заданным и, таким образом, от учащихся требуется при знаке "+" двигаться по ряду влево, а при знаке "-" - вправо.

Итак, условные обозначения чисел могут использоваться как средство повышения интереса на уроке, как средство обобщения и контроля за качеством знаний, за осознанностью их условий.

По сути дела, условные знаки - это абстрактная символика. В данном случае предлагается строить задания с условными знаками так и в такой момент обучения, чтобы они выступали не особым знанием, умением, которому надо специально учить, а лишь средством качественного овладения теми конкретными знаниями и умениями, которые предусмотрены программой.