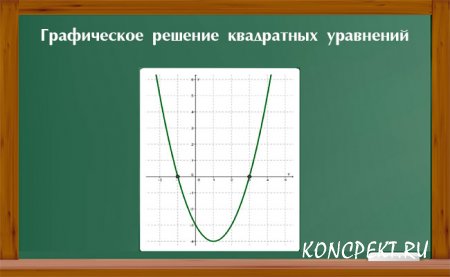
Конспект урока: Графическое решение квадратных уравнений. 8 класс

Урок сопровождается презентацией.

Урок заключительный по данной теме, учащиеся расширили свои знания о классе функций, в частности познакомились с квадратичной функцией. Сформировали представления о таких фундаментальных понятиях математики, каким являются понятия функции, ее области определения, области значения, ограниченности, непрерывности, наибольшего и наименьшего значений на заданном промежутке. Научились строить квадратичную функцию, путем параллельного переноса по оси абсцисс и по оси ординат, выделяя полный квадрат; научились строить параболу y=ax²+bx+c для любых a, b, c, знают уравнение оси симметрии параболы. На данном уроке учащиеся, используя ранее полученные знания, познакомятся с практическим применением полученных знаний, а именно научатся  решать квадратные уравнения графическим способом.

Цели урока: (слайд №2)

-     закрепить умение строить графики различных функций;

-     рассмотреть различные способы решения квадратных уравнений с помощью графиков;

-     формировать умение решать квадратные уравнения графическим способом;

-     развитие познавательного интереса;

-     воспитание у учащихся культуры графики.

Тип урока: урок изучения нового материала.

Оборудование урока: компьютеры, мульти Медео, дифференцированные карточки – задания.

План урока:

1. Организационный момент

2. Актуализация опорных знаний (слайд №3, 4)

-  Уравнение какого вида называется квадратным?

-  Как построить график функции y=af(x+l)+m  (а>1), если известен график функции y=f(x)?

-  Вверх или вниз направлены ветви параболы, если коэффициент а – отрицательный? Положительный?

-  Назовите формулу абсциссы вершины параболы. Как вычислить ординату?

-  Какая прямая является осью параболы?

-  Назовите точки ординаты, которых равны нулю.

3. Изучение нового материала (виртуальная лаборатория)

Учитель, используя виртуальную лабораторию, показывает решение квадратного уравнения x² +4x -5 =0  различными способами:

а)  Для решения данного уравнения можно построить на координатной плоскости параболу функции y=x² +4x -5  и найти точки пересечения данной параболы с осью Ох. Решением уравнения будут являться числа, соответствующие абсциссам точек пересечения.

б)  Можно часть выражения перенести на другую сторону таким образом, чтобы с одной стороны выражение составляло квадратичную функцию, а с другой стороны – линейную функцию. Например:  x² = - 4x +5; x² +4x =5; x²  -5   = - 4x .В этом случае нужно на одной координатной плоскости построить график квадратичной функции – параболу и график линейной функции – прямую. Значения абсцисс точек пересечения получившихся графиков и будут являться корнями данного уравнения.

в)  Так же можно разделить данное выражение на переменную х , получив выражение х + 4 – 5/х = 0 . В данном случае можно выражение разделить на две части, таким образом, чтобы с одной стороны осталось выражение, соответствующее линейной функции, тогда с другой стороны останется гипербола. Абсциссы точек пересечения будут решением уравнения.

Давайте ребята проанализируем, в чем суть этих способов и чем неудобен данный метод решения уравнений.

Учитель подводит учащихся к выводам, что графический способ решения уравнений не всегда удобен, т.к. точка пересечения графиков не всегда помещается на тетрадном листке и не всегда точно определяются абсциссы точек пересечения.

4. Закрепление изученного материала

Работа в группе (слайд №5)

Решить уравнение х³ – х ² – х -2 = 0.

Индивидуальная работа по карточкам на компьютерах в образовательной программе «Интерактивная геометрия»

1. Сообщение о практическом применении свойств параболы и о том, что не любое уравнение можно решить графическим способом.

2. Домашнее задание

3. Подведение итогов (слайд №6)

Графиком квадратичной функции является…

Направление ветвей параболы зависит от знака коэффициента…

Чтобы решить квадратное уравнение графическим способом нужно построить график функции и найти…

Осью симметрии параболы является прямая…

Скачать Чтобы скачать материал зарегистрируйтесь или войдите!